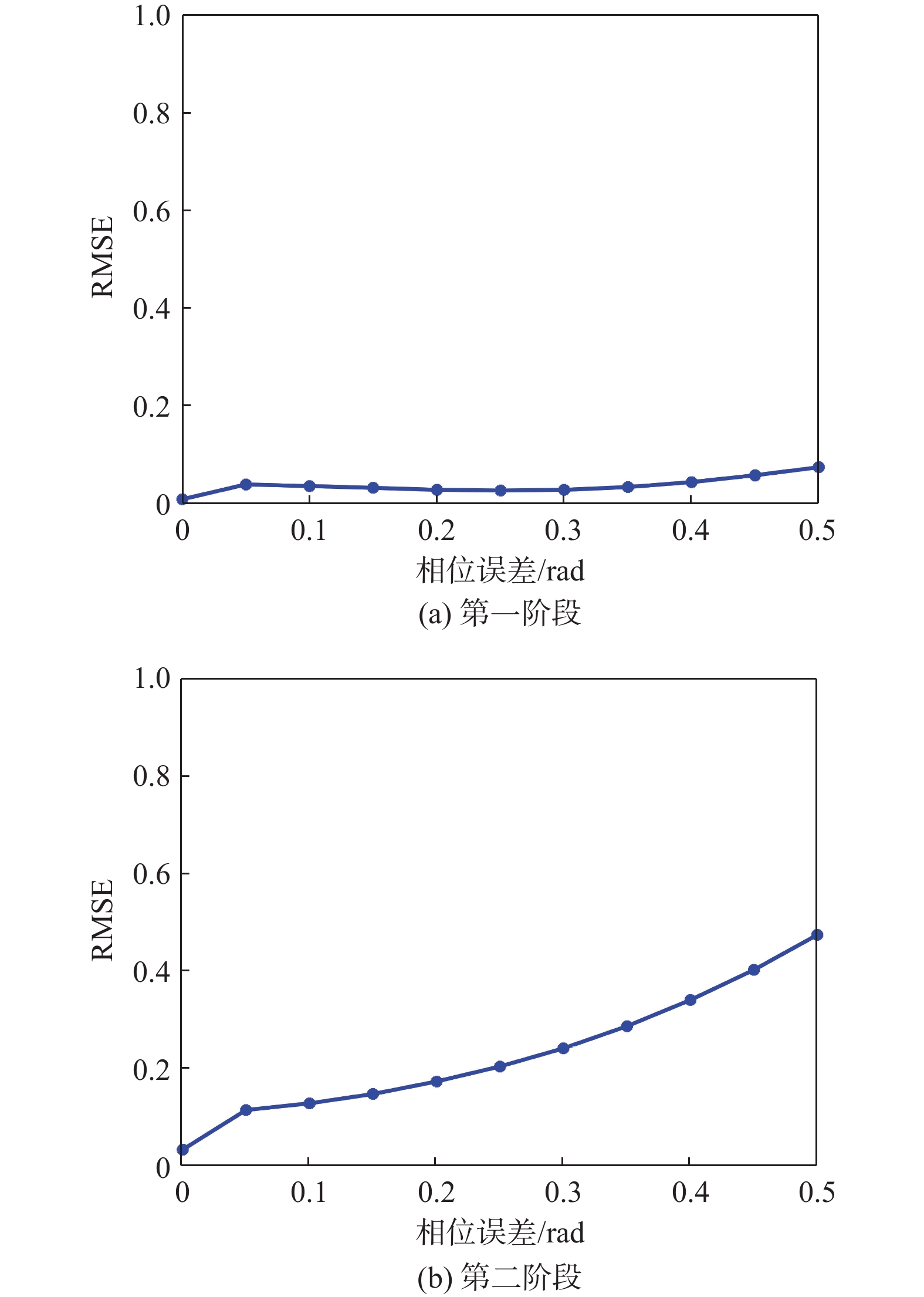
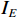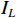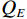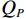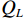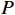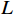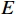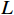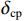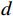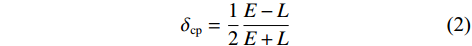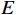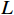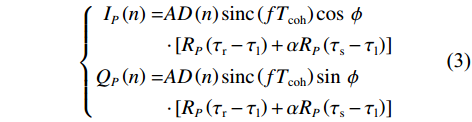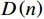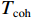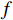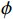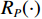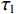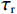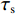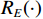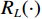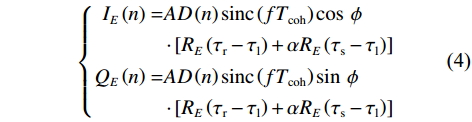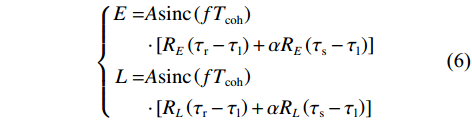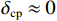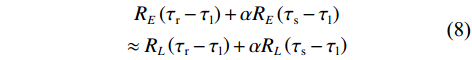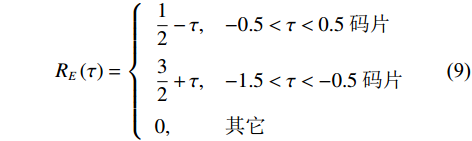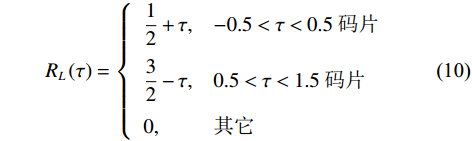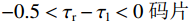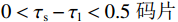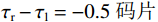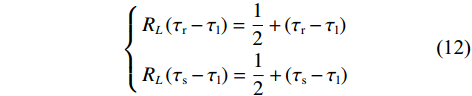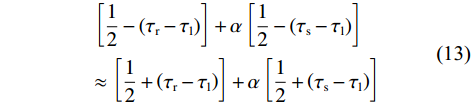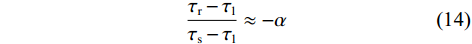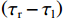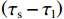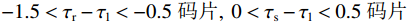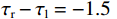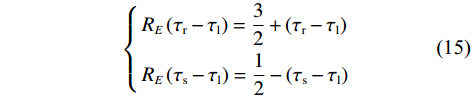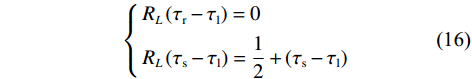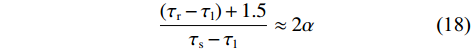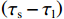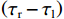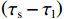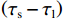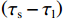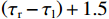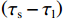The analysis of the relationship between GNSS-induced spoofing code phase and spoofing-to-signal ratio
-
摘要:
GNSS信号的强度较弱且其信号结构公开,因此易受到诱导式欺骗攻击. 此类攻击能够在接收机保持跟踪环路不失锁的条件下进行,且往往难以被实时检测. 为了深入研究诱导式欺骗的过程,提高对欺骗攻击的防御能力,重点分析了欺骗信号对接收机延迟锁定环(delay-locked loop,DLL)的影响,特别是欺骗信号对接收机码相位的牵引过程. 在假设频率锁定模式下,推导了欺骗信号与真实信号以及本地复制伪随机码之间的相对码相位差与欺信比(spoofing-to-signal ratio, SSR)的关系. 最后,通过环路仿真和GNSS接收机仿真验证了理论结果,证明了理论分析的有效性. 这一研究为提高GNSS系统的安全性与防御能力提供了理论支持.
-
关键词:
- GNSS /
- 诱导式欺骗 /
- 码相位牵引 /
- 欺信比(SSR) /
- 延迟锁定环(DLL)
Abstract:The GNSS signals are weak, their signal structure is publicly available, making them vulnerable to spoofing attacks. These attacks can occur while the receiver maintains locked on the tracking loop and are often difficult to be detected in real time. To investigate the spoofing process and enhance defense mechanisms, this study analyzes the impact of spoofing signals on the delay-locked loop (DLL) of the receiver, particularly the code phase tracking process. Under the assumption of frequency-locking mode, the relationship between the relative code phase difference of the spoofing signal and the authentic signal, as well as the locally generated pseudo-random code, is derived. This relationship is also shown to depend on the spoofing-to-signal ratio (SSR). Theoretical results are verified through loop and GNSS receiver simulations, confirming the validity of the analysis. This research provides theoretical support for improving the security and defense capabilities of GNSS systems.
-
0. 引 言
GNSS已成为现代社会的核心组成部分,广泛应用于交通、通信、金融等各个领域[1]. 然而,由于GNSS信号功率较小且格式公开,其安全性问题值得关注,尤其是在GNSS的欺骗攻击方面. 欺骗攻击通过发送伪造的GNSS信号,误导接收机产生错误的位置或时间信息,进而可能导致严重的后果[2]. 这种攻击不仅威胁到GNSS系统本身的安全性,还可能对依赖GNSS的民用应用造成巨大的损失[3-5].
根据欺骗攻击的方式,欺骗干扰可分为转发式欺骗和诱导式欺骗. 相较于转发式欺骗,诱导式欺骗通过生成虚假的卫星信号,诱使GNSS接收机将其误识别为真实卫星信号,从而导致接收机产生位置或时间计算错误,在此过程中不会导致跟踪环路失锁[6]. 由于其高度的隐蔽性和广泛的适用性,诱导式欺骗干扰已成为目前最常见的欺骗技术之一.
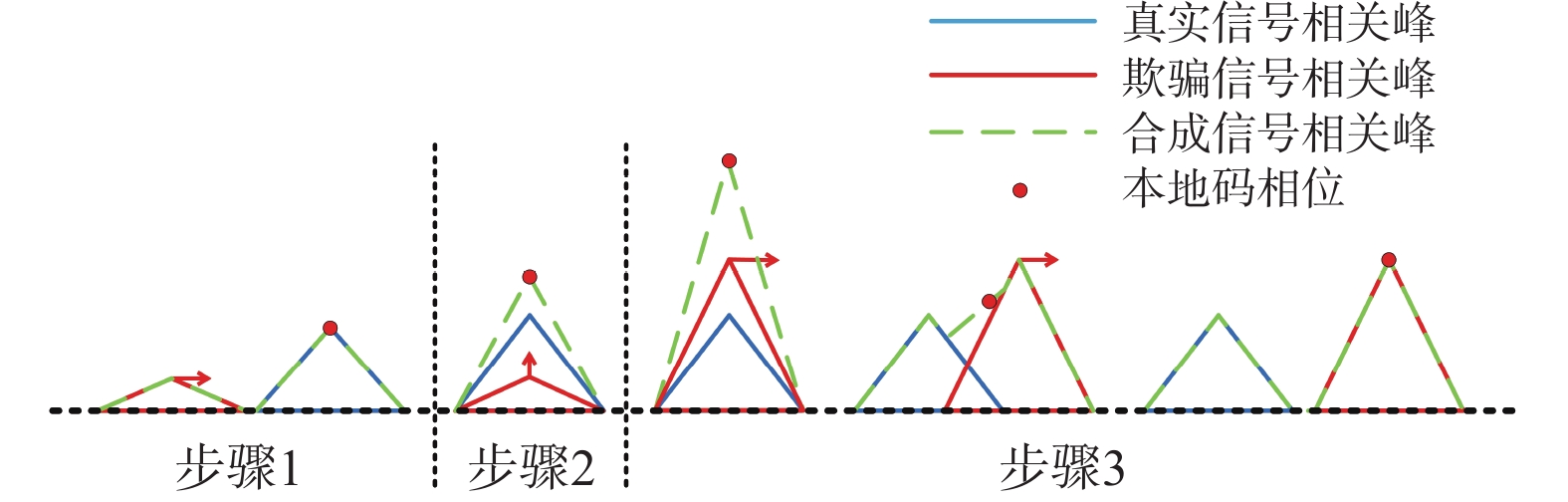
诱导式欺骗的基本原理是通过精确控制欺骗信号的参数,如码相位、载波频率和功率等,逐步引导接收机的跟踪环路偏离真实信号[7]. 图1为诱导式欺骗攻击过程,分为以下3个步骤:
步骤1:在诱导式欺骗的初期阶段,接收机稳定地跟踪真实信号,并使本地复制信号的码相位与真实信号码相位对齐. 在这一阶段,欺骗者通过大致估计真实信号的载波频率和码相位,生成一个与真实信号码相位相差若干码片且功率较低的欺骗信号,并逐步调整该欺骗信号的码相位,使其与真实信号的码相位一致.
步骤2:欺骗信号与真实信号的码相位已经对齐,欺骗者开始逐步提升欺骗信号的功率,直到其超过真实信号的功率. 通过利用功率上的优势,欺骗信号逐步接管接收机的跟踪环路.
步骤3:欺骗者进一步调整欺骗信号的码相位,使其对接收机本地复制的伪随机码相位进行牵引,直至欺骗信号与真实信号的相关峰完全分离. 此时,欺骗信号完全控制接收机的跟踪环路,诱导式欺骗成功实施.
诱导式欺骗攻击过程的第三阶段是欺骗信号与真实信号分离的重要阶段. 分离期间,欺骗信号与真实信号的相关峰相互影响,导致合成相关峰畸变,GNSS信号质量检测(signal quality monitor, SQM)技术利用相关峰的畸变以及对称性等特征对欺骗攻击进行检测[8]. 例如,Ratio度量检测相关峰的顶部畸变,而Delta度量则是检测相关峰两侧的对称性[6-9]. 此外,Wang等[10]利用三维相关函数的体积差异,结合了诱导式欺骗的动态特性来防御欺骗式干扰. 邓敏等[11]提出一种新型SQM指标,利用不同相关器输出的组合来检测欺骗干扰. 赵慎等[12-13]先后提出SQM与Ratio指标融合以及相关器输出联合功率的欺骗检测算法. 以上欺骗检测算法都是通过欺骗信号对GNSS接收机的影响来检测欺骗. 因此,为了更好地防御欺骗攻击,有必要深入地了解诱导式欺骗过程,研究欺骗信号控制目标接收机的过程. Zhou等[14]分析了欺骗信号在接管控制目标接收机延迟锁定环过程中所产生的影响,推导了欺骗成功所需的欺信比下限. 随后,Wang等[15]通过推导在存在欺骗信号的情况下码跟踪误差的变化,研究了欺骗同步误差以及接收机设置对S曲线模糊度和码跟踪轨迹的影响,进而提出了欺骗成功的必要条件.
上述方法主要关注诱导式欺骗成功的必要条件,而本文的研究重点则是诱导式欺骗攻击的过程. 本文分析了欺骗信号如何通过牵引真实信号的码相位来干扰接收机的跟踪环路. 推导了欺骗信号、真实信号与本地复制伪随机码之间的相对码相位差之间的关系. 最后,通过一系列仿真实验,验证了理论推导的正确性和实际可行性.
1. 延迟锁定环原理
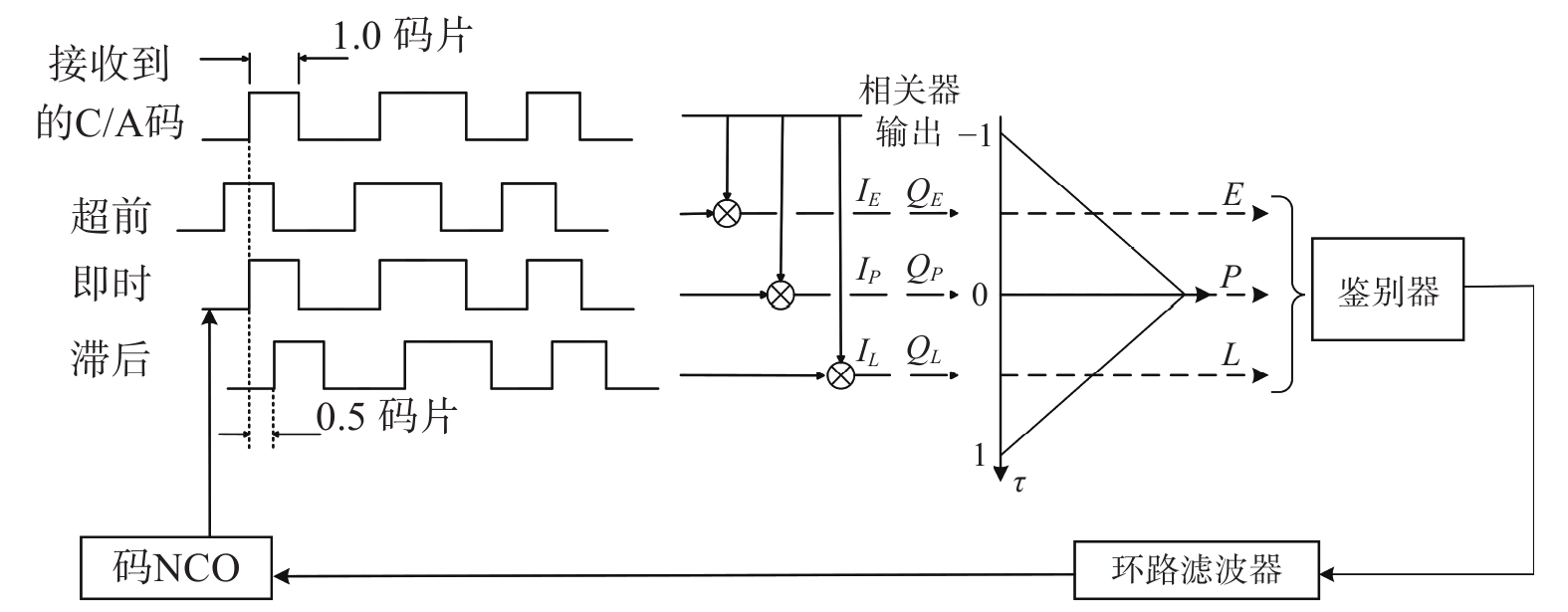
延迟锁定环(delay-locked loop,DLL)的作用是保持本地复制C/A码与接收信号C/A码相位一致,从而得到接收信号的码相位,图2为DLL的鉴相原理.
接收机的DLL在进行鉴相时,一般会复制三个不同相位的C/A码,分别为超前(Early,E)、即时(Prompt,P)和滞后(Late,L)复制C/A码,超前码的相位相对于即时码略微超前,而滞后码的相位则略微滞后于即时码. 将复制所得C/A码与接收信号进行相关运算,得到相关积分结果
${I_E}$ ,${I_P}$ ,${I_L}$ ,${Q_E}$ ,${Q_P}$ 和${Q_L}$ ,经过式(1)计算出自相关幅值$E$ ,$P$ 和$L$ .$$ \left\{ \begin{gathered} E = \sqrt {I_E^2 + Q_E^2} \\ P = \sqrt {I_P^2 + Q_P^2} \\ L = \sqrt {I_L^2 + Q_L^2} \\ \end{gathered} \right. $$ (1) DLL的鉴相原理是利用C/A码自相关函数的对称性:当
$E$ 与$L$ 相等时,便认为即时码与接收信号C/A码相位一致;否则,即时码与接收信号C/A码相位不一致,鉴别器输出复制即时码与接收信号C/A码相位差异${\delta _{{\mathrm{cp}}}}$ . 最终,该相位差通过环路滤波器反馈至C/A码数控振荡器(numerically controlled oscillator, NCO),用于生成下一时刻的本地复制C/A码. 以相关器间距$d$ 为1/2码片的常规接收机为例,码鉴相器的计算公式如下[16]:$$ {\delta _{{\mathrm{cp}}}} = \frac{1}{2}\frac{{E - L}}{{E + L}} $$ (2) DLL鉴相的本质是得到本地复制的码相位,使得自相关幅值
$E$ 和$L$ 尽可能相等,后续欺骗信号对真实信号码相位牵引过程的分析则是在此基础上展开的.2. 码相位牵引过程的理论分析
2.1 信号模型
不同的诱导式欺骗参数会对接收机产生不同的影响,其中载波相位、载波频率、码相位和欺骗信号的幅值都会影响接收机对真实信号的解算. 本文主要针对欺骗信号对接收机码相位牵引的阶段进行分析,如果同时考虑所有的参数影响很难得到有价值的结果,所以重点研究DLL中码相位和欺信比(spoofing-to-signal ratio, SSR)之间的关系. 为了防止载波环对结果的影响,假设在欺骗过程中欺骗信号载波频率和相位与真实信号始终保持一致,即频率锁定模式欺骗[17]. 当频率锁定模式欺骗进入DLL后的即时支路相干积分结果为
$$ \left\{\begin{split} I_P\left(n\right)= & AD\left(n\right)\mathrm{sin}\mathrm{c}\left(fT_{\mathrm{coh}}\right)\cos\;\phi \\ &\cdot\left[R_P\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_P\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ Q_P\left(n\right)= & AD\left(n\right)\mathrm{sin}\mathrm{c}\left(fT_{\mathrm{coh}}\right)\sin\;\phi \\ &\cdot\left[R_P\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_P\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \end{split} \right. $$ (3) 式中:
$ A $ 为真实信号幅值;$ D\left( n \right) $ 为数据码;$ {T_{{\mathrm{coh}}}} $ 为相干积分时间;$ f $ 为接收信号相对本地复制信号载波频率差;$ \phi $ 为接收信号相对本地复制信号载波相位差(由于假设欺骗信号载波频率和相位与真实信号始终保持一致,所以没有对欺骗和真实信号做区分);$ \alpha $ 为欺骗信号与真实信号的幅值比,即欺信比;$ {R}_{P}(\cdot) $ 为即时支路自相关函数,本地复制C/A码相位为${\tau _{\mathrm{l}}}$ ,真实信号的码相位为${\tau _{\mathrm{r}}}$ ,欺骗信号的码相位为${\tau _{\mathrm{s}}}$ . 超前支路和滞后支路相干积分结果与即时支路的区别仅在于其自相关值分别为$ {R}_{E}(\cdot) $ 和$ {R}_{L}(\cdot) $ ,超前支路和滞后支路相干积分结果为式(4)和式(5).$$ \left\{\begin{split} I_E\left(n\right)= & AD\left(n\right)\mathrm{sin}\mathrm{c}\left(fT_{\mathrm{coh}}\right)\cos\;\phi \\ &\cdot\left[R_E\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_E\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ Q_E\left(n\right)= & AD\left(n\right)\mathrm{sin}\mathrm{c}\left(fT_{\mathrm{coh}}\right)\sin\;\phi \\ &\cdot\left[R_E\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_E\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \end{split} \right. $$ (4) $$ \left\{\begin{split} I_L\left(n\right)= & AD\left(n\right)\mathrm{sin}\mathrm{c}\left(fT_{\mathrm{coh}}\right)\cos\;\phi \\ &\cdot\left[R_L\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_L\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ Q_L\left(n\right)= & AD\left(n\right)\mathrm{sin}\mathrm{c}\left(fT_{\mathrm{coh}}\right)\sin\;\phi \\ &\cdot\left[R_L\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_L\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \end{split} \right. $$ (5) 将式(4)和式(5)代入式(1),得到超前支路和滞后支路的自相关幅值:
$$ \left\{\begin{split} E= & A\mathrm{sin}\mathrm{c}\left(fT_{\mathrm{coh}}\right) \\ &\cdot\left[R_E\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_E\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ L= & A\mathrm{sin}\mathrm{c}\left(fT_{\mathrm{coh}}\right) \\ &\cdot\left[R_L\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_L\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \end{split} \right. $$ (6) 将上式代入式(2),得到欺骗信号输入DLL时码鉴相器的输出:
$$ \delta_{\mathrm{cp}}=\frac{1}{2}\frac{\left\{\begin{gathered}\left[R_E\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_E\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ -\left[R_L\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_L\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right]\end{gathered}\right\}}{\left\{\begin{gathered}\left[R_E\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_E\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ +\left[R_L\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_L\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right]\end{gathered}\right\}} $$ (7) DLL稳定跟踪时,码鉴相器的输出
${\delta _{{\mathrm{cp}}}} \approx 0$ ,即$$ \begin{gathered}R_E\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_E\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right) \\ \approx R_L\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+\alpha R_L\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right) \\ \end{gathered} $$ (8) 其中,超前支路和滞后支路自相关函数的表达式为
$$ {R_E}\left( \tau \right) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2} - \tau },&{ - 0.5 < \tau < 0.5\;{\mathrm{码片}}} \\ {\dfrac{3}{2} + \tau },&{ - 1.5 < \tau < - 0.5\;{\mathrm{码片}}} \\ 0,&{{\mathrm{其它}}} \end{array} } \right. $$ (9) $$ {R_L}\left( \tau \right) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2} + \tau },&{ - 0.5 < \tau < 0.5\;{\mathrm{码片}}} \\ {\dfrac{3}{2} - \tau },&{0.5 < \tau < 1.5\;{\mathrm{码片}}} \\ 0,&{{\mathrm{其它}}} \end{array} } \right. $$ (10) 2.2 码相位与SSR的关系推导
按照欺骗信号与本地码相位的关系,码相位牵引可以分为两个阶段:本地码相位远离欺骗信号;本地码相位靠近欺骗信号. 由于两个码相位牵引阶段下的真实信号和欺骗信号相关函数有所不同,所以分析过程也分为两个阶段进行.
1) 第一阶段:本地码相位远离欺骗信号阶段
$ - 0.5 < {\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}} < 0{\text{ }}{\mathrm{码片}}$ ,$0 < {\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}} < 0.5{\text{ }}{\mathrm{码片}}$ .为了便于分析,假设欺骗信号相对真实信号码相位向右移动,如图3为码相位牵引第一阶段的示意图. 在本阶段,本地复制码相位远离欺骗信号的码相位,同时本地复制码相位也远离真实信号码相位,直到本地复制码相位与真实信号码相位相距0.5 码片,即
$ \tau\mathrm{_r}-\tau\mathrm{_l}=-0.5\text{ }\mathrm{码片} $ .本阶段中超前支路和滞后支路的自相关函数为
$$ \left\{ \begin{gathered} {R_E}\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right) = \frac{1}{2} - \left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right) \\ {R_E}\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right) = \frac{1}{2} - \left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right) \\ \end{gathered} \right. $$ (11) $$ \left\{ \begin{gathered} {R_L}\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right) = \frac{1}{2} + \left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right) \\ {R_L}\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right) = \frac{1}{2} + \left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right) \\ \end{gathered} \right. $$ (12) 将式(11)和式(12)代入式(8)中得
$$ \begin{gathered}\left[\frac{1}{2}-(\tau_{\mathrm{r}}-\tau_{\mathrm{l}})\right]+\alpha\left[\frac{1}{2}-\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ \approx\left[\frac{1}{2}+\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)\right]+\alpha\left[\frac{1}{2}+\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ \end{gathered} $$ (13) 经过化简得到
$$ \frac{\tau_{\mathrm{r}}-\tau_{\mathrm{l}}}{\tau_{\mathrm{s}}-\tau_{\mathrm{l}}}\approx-\alpha $$ (14) 式(14)表示在码相位牵引第一阶段中,真实信号与本地复制码相位差
$\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right)$ 和欺骗信号与本地复制码相位差$\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right)$ 之比等于SSR的相反数.2) 第二阶段:本地码相位靠近欺骗信号阶段
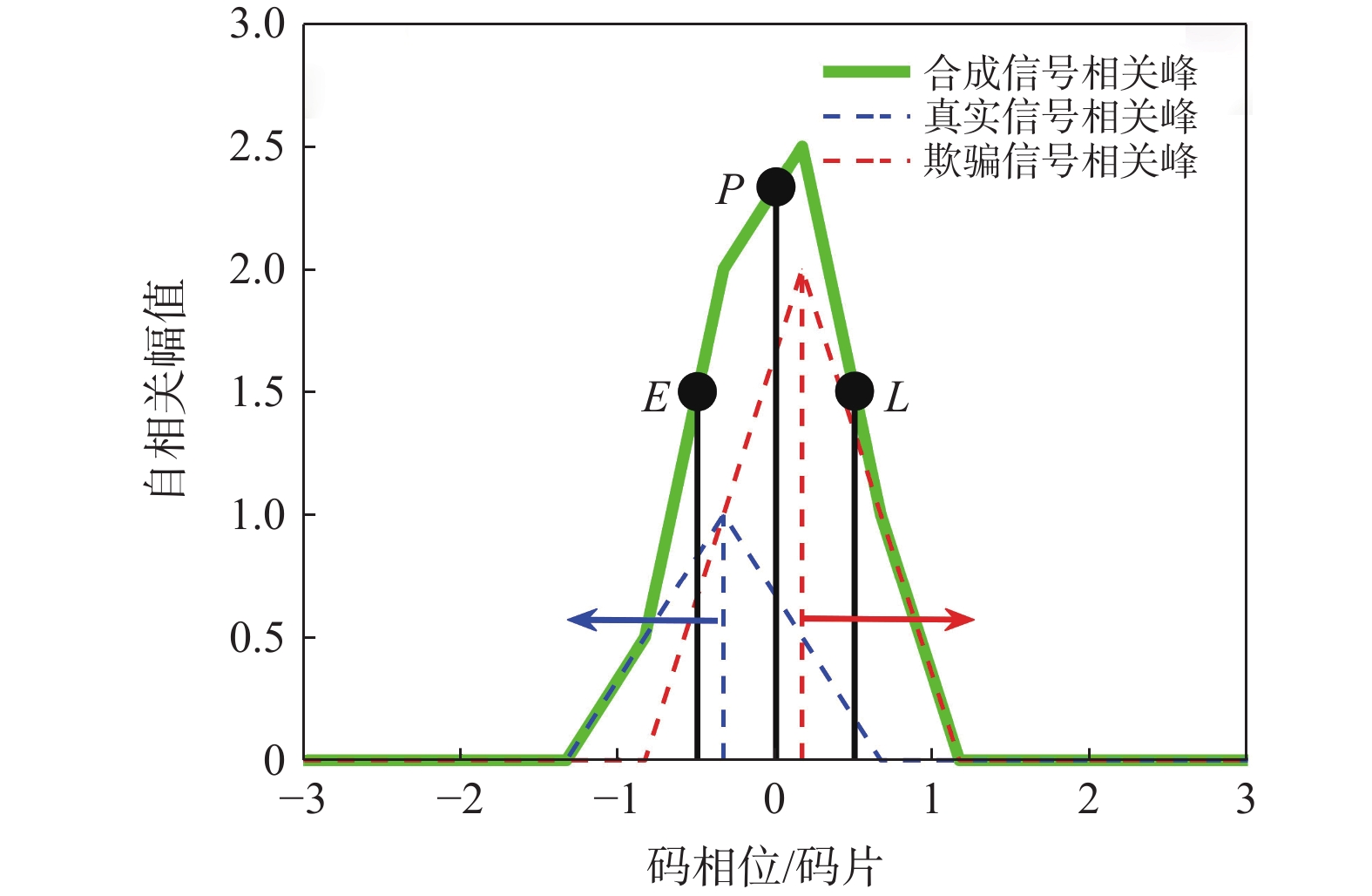
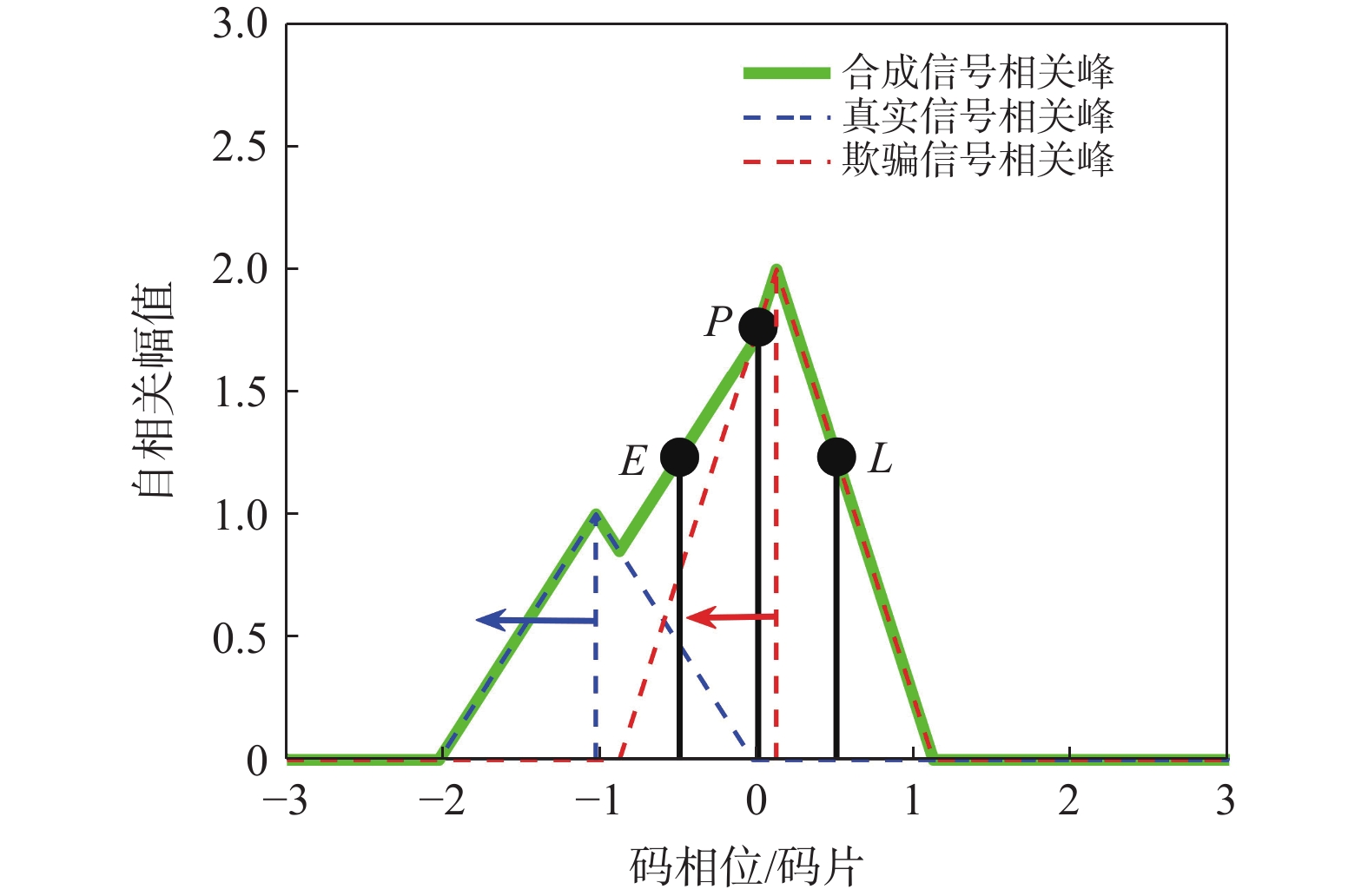
$ - 1.5 < {\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}} < - 0.5{\text{ }}{\mathrm{码片}},{\text{ }}0 < {\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}} < 0.5{\text{ }}{\mathrm{码片}}$ .图4为码相位牵引第二阶段的示意图,在本阶段,本地复制码相位不断靠近欺骗信号的码相位,而远离真实信号码相位,直到本地复制码相位与真实信号码相位相距1.5 码片,即
$ \tau_{\mathrm{r}}-\tau_{\mathrm{l}}=-1.5\text{ }$ 码片.本阶段中超前支路和滞后支路的自相关函数为
$$ \left\{ \begin{gathered} {R_E}\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right) = \frac{3}{2} + \left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right) \\ {R_E}\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right) = \frac{1}{2} - \left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right) \\ \end{gathered} \right. $$ (15) $$ \left\{ \begin{gathered} {R_L}\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right) = 0 \\ {R_L}\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right) = \frac{1}{2} + \left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right) \\ \end{gathered} \right. $$ (16) 将式(15)和式(16)代入式(8)中得
$$ \begin{gathered}\left[\frac{3}{2}+\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)\right]+\alpha\left[\frac{1}{2}-\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ \approx\alpha\left[\frac{1}{2}+\left(\tau_{\mathrm{s}}-\tau_{\mathrm{l}}\right)\right] \\ \end{gathered} $$ (17) 经过化简得到
$$ \frac{\left(\tau_{\mathrm{r}}-\tau_{\mathrm{l}}\right)+1.5}{\tau_{\mathrm{s}}-\tau_{\mathrm{l}}}\approx2\alpha $$ (18) 式(18)表示在码相位牵引第二阶段中,真实信号与本地复制码相位差
$\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right)$ 加1.5 码片和欺骗信号与本地复制码相位差$\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right)$ 之比等于SSR的2倍.3. 仿真验证与分析
3.1 环路仿真
本节利用理想信号进行仿真验证,仿真信号中仅包含C/A码,载波以及信号幅度,不包含导航电文和噪声. SSR设置为2,欺骗信号与真实信号的载波频率始终保持一致,仅对DLL进行码相位欺骗,即频率锁定模式.
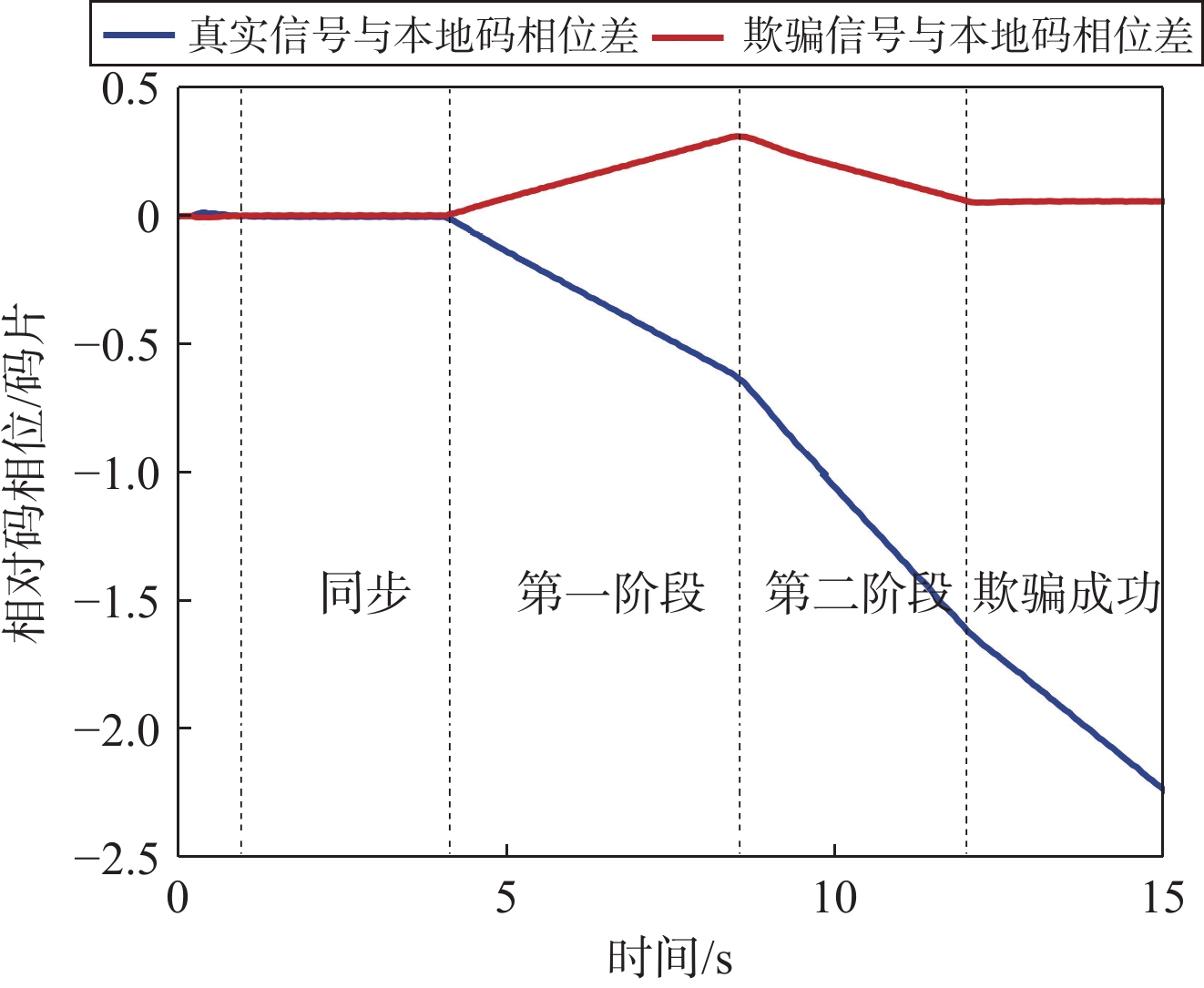
仿真验证重点研究码相位牵引过程,所以仿真针对欺骗相关峰和真实相关峰分离部分. 仿真数据总时间为15 s,第1 s加入欺骗信号,经过3 s码相位同步,在第4 s开始进行匀速码相位牵引,直到第15 s牵引结束,最终欺骗信号与真实信号码相位相距2.2 码片. 图5为码相位牵引过程.
图6中,通过DLL输出得到真实信号与本地复制码相位差与真实信号与本地复制码相位差随时间变化.
由图6可以看出,在码相位牵引第一阶段,欺骗信号与本地复制码的相对相位差在增大,真实信号与本地复制码的相对相位差也在增大;在码相位牵引第二阶段,欺骗信号与本地复制码的相对相位差开始减小,而真实信号与本地复制码的相对相位差依然增大;最终本地复制码相位与欺骗信号同步,欺骗信号接管接收机的DLL,欺骗成功.
下面验证在码相位牵引的两个阶段中相对码相位差与SSR之间的关系.
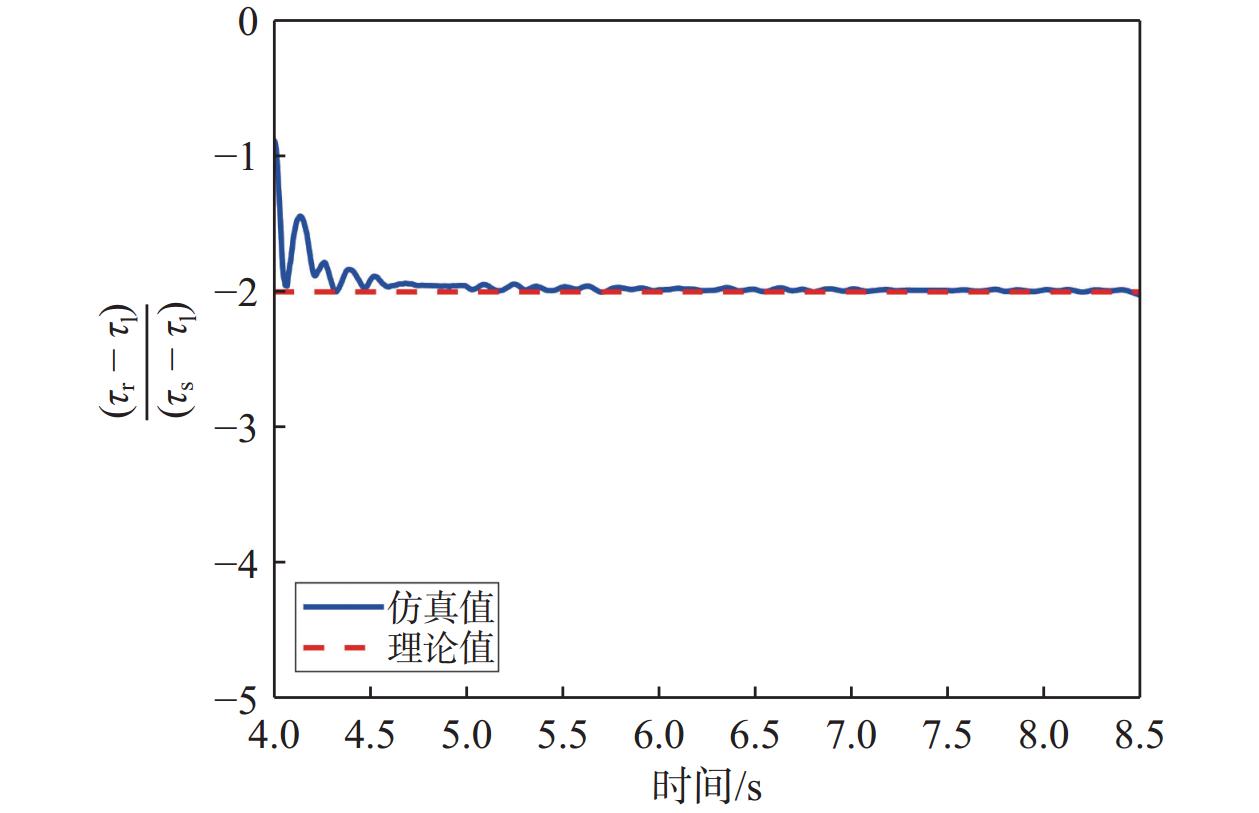
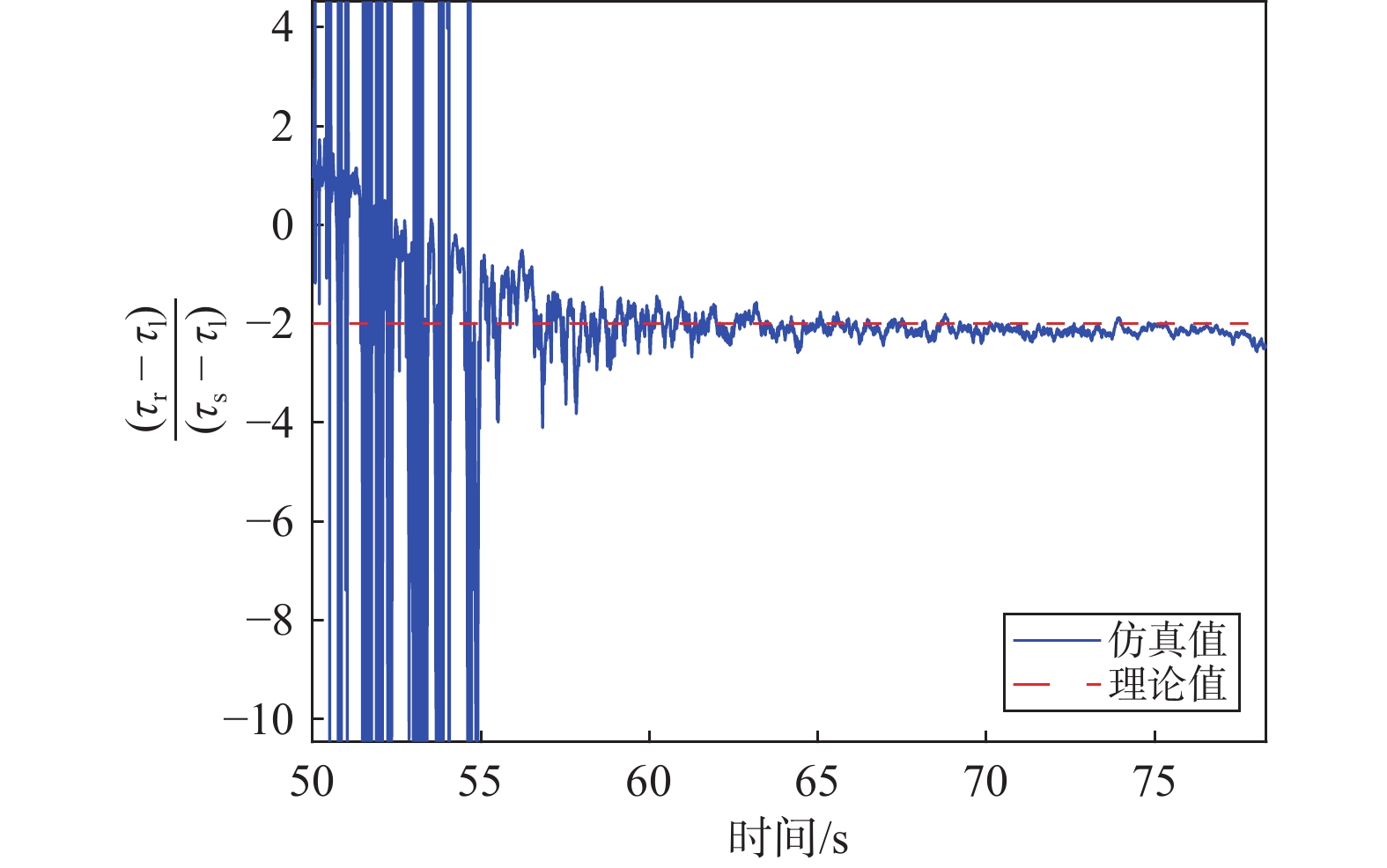
1) 第一阶段:利用真实信号与本地复制码相位差
$\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right)$ 除以欺骗信号与本地复制码相位差$\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right)$ 的比值和理论值(SSR的相反数,值为−2)对比,结果如图7所示.从图7中的对比结果可以看出,仿真值与理论值之间的差异较小,仿真值基本稳定地波动在理论值附近. 这表明,在第一阶段,所建立的模型与实际仿真结果相符,验证了所推导相对码相位差与SSR之间的关系的正确性.
2) 第二阶段:利用
$\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right) + 1.5$ 与$\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right)$ 的比值和理论值(SSR的2倍,值为4)对比,结果如图8所示.图8的结果显示,仿真值与理论值之间的差异较小,并且仿真值稳定在理论值附近,证明了第二阶段的推导结果是正确的,进一步验证了模型的有效性和精确性.
3.2 GNSS接收机仿真
本节利用卫星信号模拟器生成频率锁定模式欺骗进行仿真实验. 欺骗信号与真实信号的载波频率始终保持一致,欺骗的功率优势为3 dB(SSR=2).
图9为卫星信号模拟器仿真频率锁定模式欺骗数据输入接收机,环路输出得到真实信号与本地复制码相位差和真实信号与本地复制码相位差随时间的变化. 码相位牵引的过程同样分为两个阶段,与上一节中环路仿真结果一致.
下面在码相位牵引的两个阶段中分别验证相对码相位差与SSR之间的关系.
1) 第一阶段:利用真实信号与本地复制码相位差
$\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right)$ 除以欺骗信号与本地复制码相位差$\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right)$ 的比值和理论值(SSR的相反数,值为−2)对比,结果如图10所示.从图10可以看到,在第一阶段初期,由于真实信号与欺骗信号的码相位比较接近,相关峰之间相互影响导致仿真值存在较大的波动. 随着时间的推移,环路稳定,仿真值逐渐接近理论值. 这表明,在更加真实的欺骗场景下,理论推导依然具有有效性.
2) 第二阶段:利用
$\left( {{\tau _{\mathrm{r}}} - {\tau _{\mathrm{l}}}} \right) + 1.5$ 与$\left( {{\tau _{\mathrm{s}}} - {\tau _{\mathrm{l}}}} \right)$ 的比值和理论值(SSR的2倍,值为4)对比,结果如图11所示.图11中的对比结果进一步验证了这一点,仿真值几乎稳定在理论值附近,表明仿真模型的推导结果是有效的,能够验证欺骗信号接管接收机环路的过程.
3.3 误差分析
在实际欺骗场景中,欺骗者并不能准确的获取真实信号的多普勒频率以及载波相位信息,所以频率锁定模式欺骗信号的多普勒频率和载波相位无法与真实信号保持严格一致. 为了使理论分析更加接近实际欺骗场景,本节分析了欺骗信号与真实信号同步过程中产生的多普勒频率误差以及载波相位误差对理论推导结果的影响.
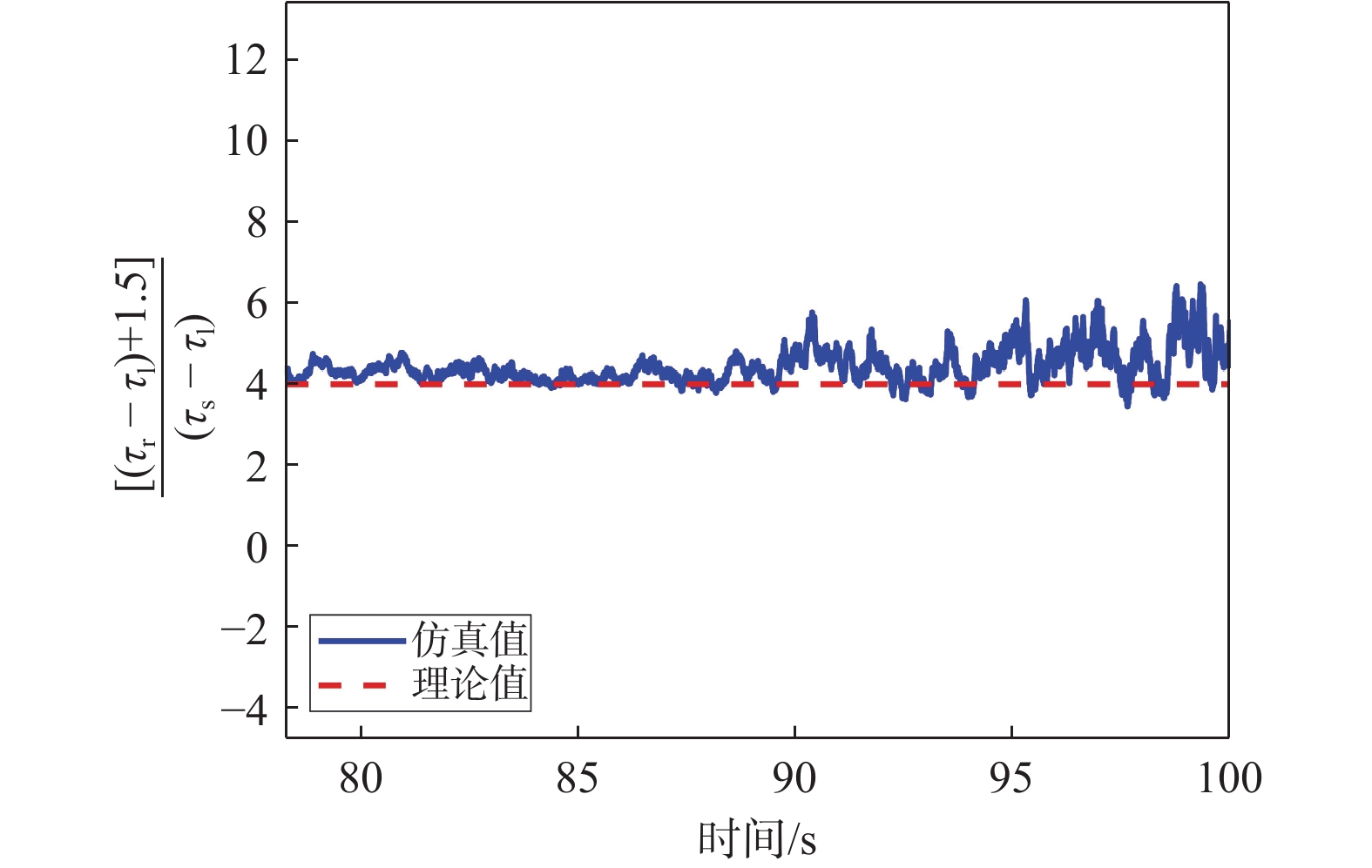
为了衡量同步过程中多普勒频率误差与载波相位误差对结果的影响,利用均方根误差(root mean squared error,RMSE)来评价仿真值与理论值之间的差异. RMSE越接近0,表示仿真值与理论值之间的误差越小. 本节实验在不同多普勒频率误差和载波相位误差下得到仿真值与理论值的RMSE,其他实验条件均与前文保持一致. 图12 (a)和(b)分别为码相位分离的两个阶段不同多普勒频率误差下仿真值与理论值的RMSE.
图12中的结果显示在码相位分离的两个阶段仿真值与理论值的RMSE均未超过0.7,表明在误差范围一定的情况下,理论值的推导具有较高的准确性.
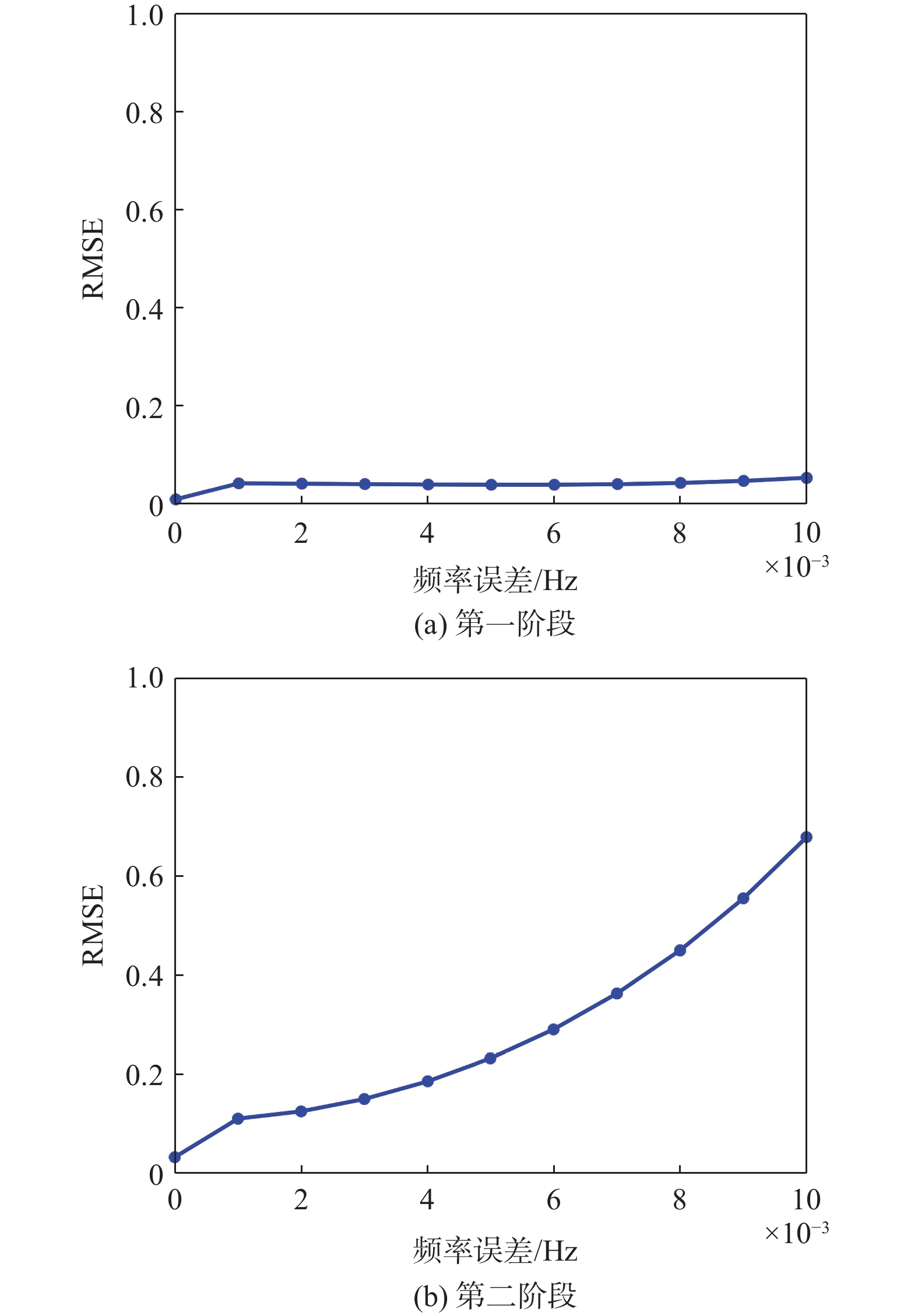
图13 (a)和(b)分别为码相位分离的两个阶段不同载波相位误差下仿真值与理论值的RMSE.
图13中的结果显示在不同载波相位误差下的两个阶段仿真值与理论值的RMSE均未超过0.5,同样证明了理论值的推导在载波相位误差影响下的有效性.
4. 结束语
本文针对诱导式欺骗对GNSS接收机的诱导过程进行了系统研究,重点分析了诱导式欺骗对DLL中的码相位牵引过程的影响. 通过对欺骗信号与真实信号在码相位牵引过程中的相对变化进行理论分析,推导了相对码相位差与SSR之间的关系,利用环路仿真和GNSS接收机仿真对理论结果进行了验证,并对频率误差和相位误差进行了分析. 实验结果表明,在欺骗信号成功接管接收机跟踪的过程中,相对码相位差与SSR之间的满足理论推导的定量关系. 仿真数据与理论推导结果一致,验证了所提理论的有效性和精确性. 本文的研究成果为理解诱导式欺骗攻击的工作机制提供了更深入的理论支持,也为GNSS接收机防御措施的改进提供了理论依据.
-
[1] BIAN S, HU Y, JI B. Research status and prospect of GNSS anti-spoofing technology[J]. Scientia sinica informationis, 2017, 47(3): 275-287. DOI: 10.1360/N112016-00073
[2] JAFARNIA-JAHROMI A, BROUMANDAN A, NIELSEN J, et al. GPS vulnerability to spoofing threats and a review of antispoofing techniques[J]. International journal of navigation and observation, 2012(1): 127072. DOI: 10.1155/2012/127072
[3] AMIN M G, CLOSAS P, BROUMANDAN A, et al. Vulnerabilities, threats, and authentication in satellite-based navigation systems[J]. Proceedings of the IEEE, 2016, 104(6): 1169-1173. DOI: 10.1109/JPROC.2016.2550638
[4] JAFARNIA-JAHROMI A, BROUMANDAN A, DANESHMAND S, et al. Vulnerability analysis of civilian L1/E1 GNSS signals against different types of interference[C]//Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2015), 2015: 3262-3271.
[5] 吴长柯, 侯强. 无人机GNSS诱骗与反诱骗技术论述[J]. 全球定位系统, 2020, 45(3): 37-40. [6] PHELTS R E. Multicorrelator techniques for robust mitigation of threats to GPS signal quality[D]. USA: Stanford University, 2001.
[7] GAO Y J, LV Z W, ZHANG L D. Asynchronous lift-off spoofing on satellite navigation receivers in the signal tracking stage[J]. IEEE sensors journal, 2020, 20(15): 8604-8613. DOI: 10.1109/JSEN.2020.2984525
[8] PSIAKI M L, HUMPHREYS T E. GNSS spoofing and detection[J]. Proceedings of the IEEE, 2016, 104(6): 1258-1270. DOI: 10.1109/JPROC.2016.2526658
[9] PINI M, FANTINO M, CAVALERI A, et al. Signal quality monitoring applied to spoofing detection[C]//Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), 2011: 1888-1896.
[10] WANG W Y, HOU Y L. GNSS induced spoofing detection based on dynamic three-dimensional correlation function[J]. IEEE transactions on instrumentation and measurement, 2024, 73. DOI: 10.1109/TIM.2024.3472768
[11] 邓敏, 廖欣璐, 郭莹莹, 等. 基于新型SQM的GNSS欺骗式干扰检测技术[J]. 全球定位系统, 2024, 49(4): 56-65. DOI: 10.12265/j.gnss.2024017 [12] 赵慎, 胡勇, 李世玲, 等. 基于PCS与Ratio融合的GNSS欺骗检测方法研究[J]. 全球定位系统, 2024, 49(4): 99-106. [13] 赵慎, 廖一霏, 李世玲, 等. 多相关器联合功率GNSS欺骗干扰检测方法研究[J]. 全球定位系统, 2024, 49(4): 66-74. DOI: 10.12265/j.gnss.2023235 [14] ZHOU M, LIU Y, LIN X, et al. Performance analysis of spoofing signal ratio for receiver-spoofer[C]//Proceedings of the 2017 International Technical Meeting of The Institute of Navigation, 2017: 898-911.
[15] WANG Y W, KOU Y H, HUANG Z G. Necessary condition for the success of synchronous GNSS spoofing[J]. Chinese journal of electronics, 2023, 32(3): 438-452. DOI: 10.23919/cje.2021.00.307
[16] 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009. [17] 申成良. GPS接收机抗欺骗式干扰实验研究[D]. 成都: 电子科技大学, 2018.



 下载:
下载: