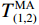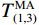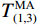P-wave phase identification with combined CEEMD and improved modified energy ratio for high frequency GNSS co-seismic placements
-
摘要:
针对高频GNSS同震位移在P波震相拾取存在精度低、适应性差、易出错等缺陷,提出了一种联合完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMD)和改进修正能量比(IMER)的高频GNSS同震位移P波震相识别方法,以克服高频GNSS同震位移的低信噪比、非平稳性对P波震相拾取的影响. 该方法利用CEEMD将小波阈值去噪后的高频GNSS同震波形进行分解,得到若干个本征模态分量(intrinsic mode function,IMF),利用多尺度排列熵(multi-scale permutation entropy,MPE)对IMF分量进行频带分组,并对高频分量进行信号重构,最后利用IMER方法对重构信号进行P波初至的准确拾取. 采用美国加利福尼亚州Ridgecrest地区震时台站高频GNSS数据为研究对象,对获取的同震位移和速度波形进行P波初至拾取. 结果表明,与三种传统方法相比,本文方法对P波初至拾取精度最高,可为地震预警、震后灾害快速评估等提供技术支撑.
-
关键词:
- 高频GNSS /
- 同震位移 /
- 完备集合经验模态分解(CEEMD) /
- 震相识别 /
- 地震预警
Abstract:In view of the shortcomings of low accuracy, poor adaptability, and error-prone P-wave phase picking in high-rate GNSS co-seismic displacements, a method combining complete ensemble empirical mode decomposition (CEEMD) and improved modified energy ratio (IMER) for high-rate GNSS co-seismic displacement P-wave phase identification is proposed to overcome the impact of low signal-to-noise ratio (SNR) and non-stationarity on P-wave phase picking. This method first decomposes the high-rate GNSS co-seismic waveform after wavelet threshold denoising using CEEMD to obtain several intrinsic mode functions (IMFs). Then, multiscale permutation entropy (MPE) is used to group the IMF components into frequency bands, and the signal is reconstructed from the high-frequency components. Finally, the IMER method is applied to accurately pick up the first arrivals of the P-wave in the reconstructed signal. The method is tested using high-rate GNSS data from seismic stations in the Ridgecrest area of California, USA, to pick up the P-wave first arrivals from the acquired co-seismic displacement and velocity waveforms. The results show that, compared with the three traditional methods, CEEMD-IMER has the highest accuracy of P-wave first arrivals pickup and can provide technical support for the early warning of earthquakes and rapid assessment of post-earthquake disasters.
-
0. 引 言
近年来,随着GNSS技术的飞速发展,高频GNSS能够快速准确获取包含永久形变的地表位移,弥补了传统观测手段在强震级(M>7)地震中出现的震级饱和、积分后基线偏移等缺陷,已成为当前地震大地测量学领域的研究热点[1-7].
高频GNSS同震位移包含了丰富的临震信息,P波初至的自动准确拾取对地震预警参数的快速获取至关重要[8-9]. 然而,P波常淹没于高频GNSS观测数据的噪声中,为震相准确拾取带来极大困难. 对于地震事件,已发展了多种时域类震相自动拾取方法,如长/短时窗均值比(long term average/short term average,LTA/STA)[10]、基于自回归模型(autoregressive model,AR)的赤池信息准则法(Akaike information criterion,AIC)[11]、改进的修正能量比(IMER)[12]等. 相比于前两种方法,IMER应用了三窗口算法,可有效减弱信号中噪声带来的影响. 此外,天然地震会导致短周期地震波中存在随时间变化的特征,因此可将信号分解到不同的时间尺度上. 文献[13]将高频GNSS信号进行小波变换,重构包含地震信号的第6到第8细节分量用于人工地震检测. 然而,小波变换本质上是线性非自适应变换,因此不适合处理具有非线性特征的信号[14],而经验模态分解(empirical mode decomposition,EMD)无需设置“基函数”,可自适应地将非线性信号分解为从高频到低频的IMF. 文献[15]结合EMD与AIC(EMD-AIC)对1938个地震仪微震信号进行P波到时拾取,表明利用第5个IMF分量进行拾取的结果与手动拾取差异最小. 但EMD存在模态混叠效应,为了解决该问题,EMD已经发展到完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMD)[16].
为此,本文提出了一种联合CEEMD和IMER(CEEMD-IMER)的高频GNSS同震位移P波震相识别方法,以提高高频GNSS同震波形中P波初至自动拾取的准确率. 为了将EMD-AIC方法用于高频GNSS,本文将该方法改进为C-LTA/STA+ARAIC方法,首先采用CEEMD进行信号重构,最后利用LTA/STA+ARAIC方法对重构信号进行拾取. 对2019年美国加利福尼亚州Ridgecrest地区Mw7.1级地震时14个台站记录的高频(5 Hz)GNSS数据进行定位解算,分别获取GNSS台站速度与位移波形,利用本文方法进行P波到时拾取,并同三种传统方法(包括IMER、LTA/STA+ARAIC和C-LTA/STA+ARAIC)比较,以验证本文方法的有效性和可靠性.
1. 联合CEEMD和IMER的P波震相识别方法
1.1 CEEMD方法
CEEMD能够很好地降低重构信号中的残余辅助噪声[17]. 原始GNSS地震信号X(t)经CEEMD分解后可获得N个依次从高频到低频的本征模态分量(intrinsic mode function,IMF),其分解步骤如下:
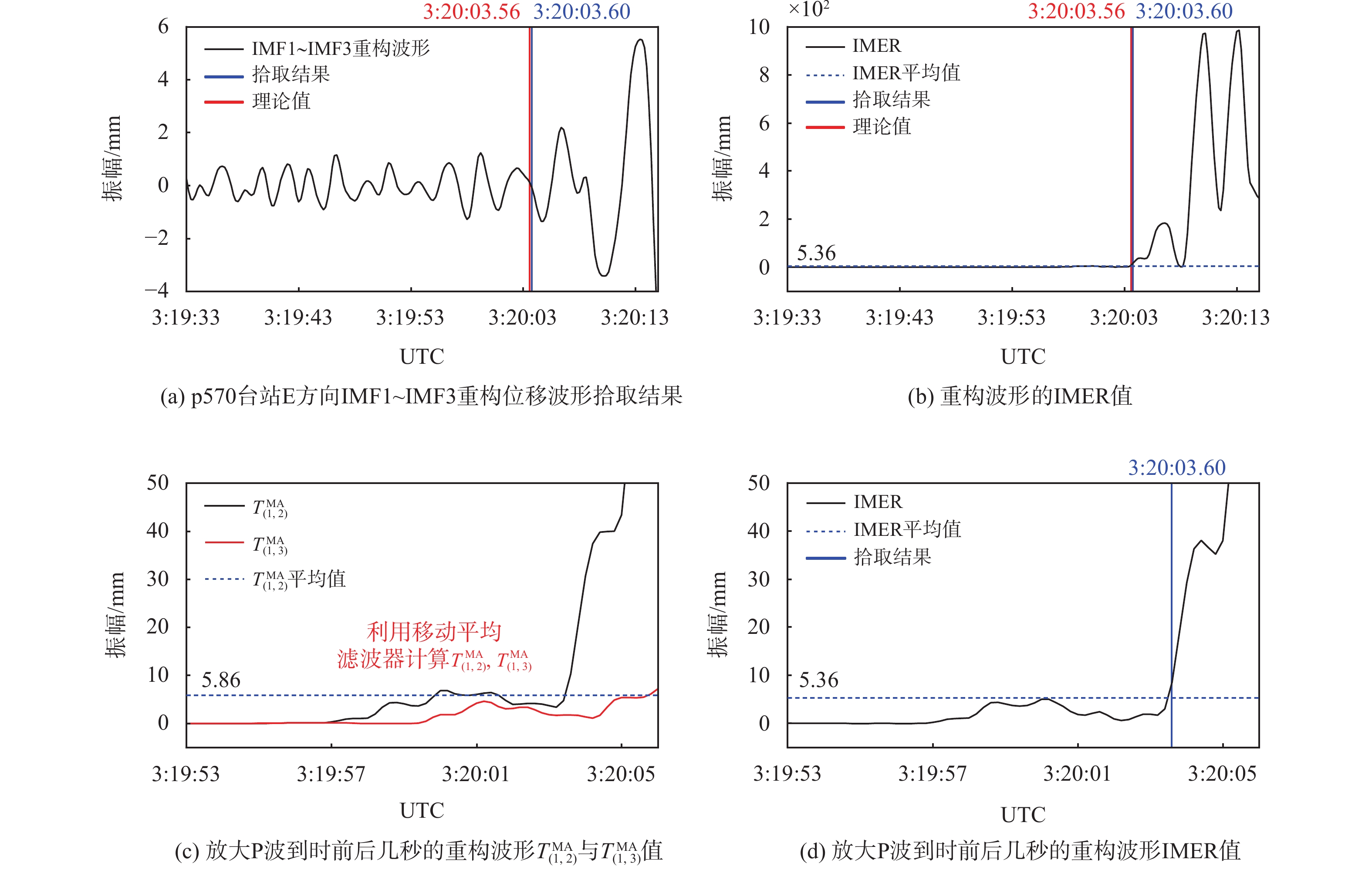
1) 定义算子Ej(·)为信号通过EMD分解得到的第j个IMF;Cj为CEEMD分解得到的第j个IMF;rj为第j个残余分量. 向地震信号X(t)中加入M次不同的高斯白噪声
${\mu _i}$ 后进行EMD分解,相应公式如下:$$ {C_{n + 1}} = \frac{1}{M}\sum\limits_{i = 1}^M {{E_1}({r_n} + {\varepsilon _i}{E_n}({\mu _i}))} $$ (1) $$ {r_n} = {r_{n - 1}} - {C_n} $$ (2) 式中:
$ n = 2,3, \cdots ,N $ ;${\varepsilon _i}$ 为噪声系数;C1和C2为$$ {C_1} = \frac{1}{M}\sum\limits_{i = 1}^M {{E_1}(X(t) + {\varepsilon _i}{\mu _i})} $$ (3) $$ {C_2} = \frac{1}{M}\sum\limits_{i = 1}^M {{E_1}({r_1} + {\varepsilon _i}{E_1}({\mu _i}))} $$ (4) 第一个残余分量r1为
$$ {r_1} = X(t) - {C_1} $$ (5) 2) 循环计算Cn+1,当残余分量极值点数量少于2时,停止分解,结果可表示为
$$ X(t) = \sum\limits_{i = 1}^N {{C_i}} $$ (6) 对地震波来说,体波的频率范围约为0.02~100 Hz,地震首波(P波)通常是高频信号[18]. 若要对P波初至进行准确拾取,就要尽可能减轻高频和低频噪声的影响[13]. 为此,本文方法首先对高频GNSS同震位移进行小波去噪,以减少噪声扰动.
为更好重建高频地震信号,本文将结合多尺度排列熵(multi-scale permutation entropy,MPE)对IMF分量进行频带分组[19-20],计算不同尺度因子s下各IMF分量的排列熵H:
$$ H = - \sum\limits_{r = 1}^R {P_r^s\ln P_r^s} $$ (7) 式中:
$P_r^s$ 为每种排列类型在尺度因子为s时出现的概率;$r = 1,2, \cdots ,R,R \leqslant m!$ ;m为嵌入维数. 当$P_r^s = 1/m!$ 时,H达到最大值ln(m!). 对尺度s下时间序列的排列熵进行归一化,得到MPE值h:$$ h = H/\ln (m!) $$ (8) 将归一化后的MPE值作为高频IMF分量和低频IMF分量的分界依据[21]. 通常,将MPE值大于0.6的IMF视为高频分量[22].
1.2 IMER方法
IMER方法[12]是在修正能量比法(MER)的基础上增加了第三个窗口计算信号中噪声部分的MER值,以消除与信号形式相似且在地震波初至前存在的噪声,以及对每个MER值数据点应用移动平均滤波器以消除高频波动. 将最终IMER值的平均值作为阈值标准识别微震信号的到达时间,若信号噪声水平较高,可取2~3倍的平均值作为新的阈值标准. 相应公式如下:
$$ T_{k(1,2)}^{\text{E}} = \frac{{\displaystyle\sum\limits_{j = k}^{k + {n_{{t}}}_1} {X_j^2} }}{{\displaystyle\sum\limits_{j = k - n_{t2}}^k {X_j^2} }} $$ (9) $$ T_{k(1,2)}^{\text{M}} = {[T_{k(1,2)}^{\text{E}} \cdot |{X_k}|]^3} $$ (10) $$ T_{i(1,3)}^{\text{E}} = \frac{{\displaystyle\sum\limits_{j = i + {n_{{t}}}_2}^{i + {n_{{t}}}_1 + {n_{{t}}}_2} {X_j^2} }}{{\displaystyle\sum\limits_{j = i - {n_{{t}}}_3}^i {X_j^2} }} $$ (11) $$ T_{i(1,3)}^{\text{M}} = {[T_{i(1,3)}^{\text{E}} \cdot |{X_i}|]^3} $$ (12) 式中:nt1、nt2和nt3分别代表第一、第二和第三时窗的采样点数,其中nt1<nt2=nt3;k、i分别是第一和第二、第一和第三时窗之间的测试点,
$ k,i = 1,2,3, \cdots ,n $ ;$T_{k(1,2)}^{\text{E}}$ 、$T_{k(1,2)}^{\text{M}}$ 分别是k处的第一和第二时窗的能量比值、MER值,$T_{i(1,3)}^{\text{E}}$ 、$T_{i(1,3)}^{\text{M}}$ 是i处第一和第三时窗的比值;Xk、Xi分别为k、i处的地震信号幅值;分别对$T_{k(1,2)}^{\text{M}}$ 、$T_{i(1,3)}^{\text{M}}$ 采用4~10个采样点数的移动平均滤波器得到$T_{(1,2)}^{{\text{MA}}}$ 、$T_{(1,3)}^{{\text{MA}}}$ ,相减可得$$ {I_j} = T_{j(1,2)}^{{\text{MA}}} - T_{j - {n_{t2}}(1,3)}^{{\text{MA}}} $$ (13) 式中:
$ {I_j} $ 表示j处的IMER值$(j= {n_{{{t2}}}} + 1,{n_{{{t2}}}} + 2, \cdots ,n) $ ;$ T_{j(1,2)}^{{\text{MA}}} $ 、$ T_{j(1,3)}^{{\text{MA}}} $ 分别为j处的$T_{(1,2)}^{{\text{MA}}}$ 、$T_{(1,3)}^{{\text{MA}}}$ .1.3 算法流程
综上,如图1所示,CEEMD驱动的P波震相拾取方法实现步骤为:
1) 对高频GNSS地震波形进行小波降噪处理;
2) 利用CEEMD将去噪后的波形分解得到N个IMF分量;
3) 计算不同尺度因子下各IMF分量的排列熵均值作为MPE值,并根据MPE值进行频带分组,选出高频分量后进行叠加得到重构信号;
4) 对重构信号使用IMER方法进行震相初至拾取.
2. 高频GNSS数据处理与解算
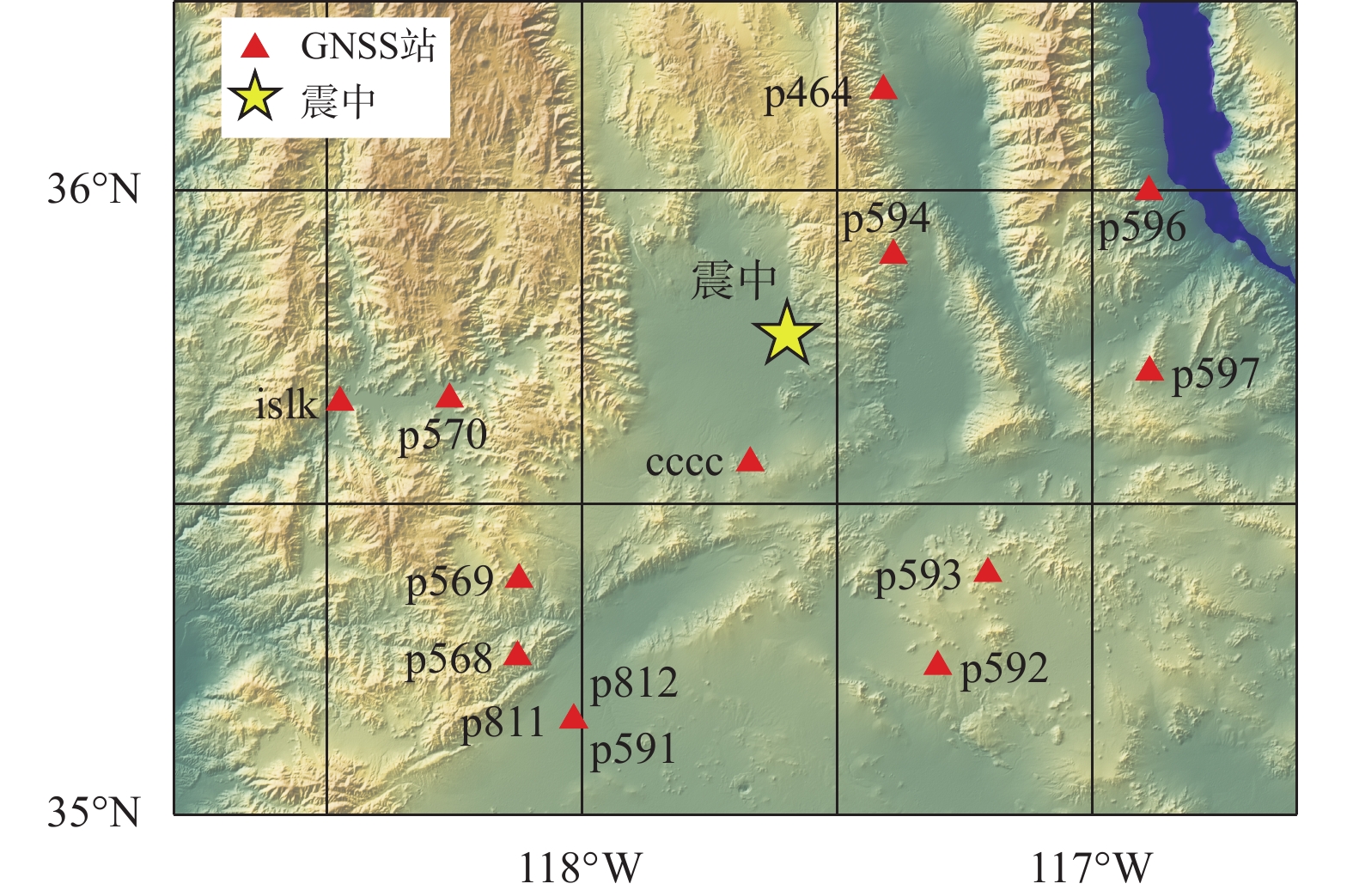
2019年7月6日03:19:53(UTC) Ridgecrest地区发生Mw7.1级地震,震中位于(35.770°N,117.599°W). 本文选取了震中附近14个高频(5 Hz)GNSS台站数据,如图2所示.
本文采用SNIVEL软件包[23]进行历元间载波相位差分解算得到GNSS同震速度波形;利用武汉大学GNSS中心的PRIDE PPP-AR (precise point positioning with ambiguity resolution,PPP-AR)软件包[24]进行精密单点定位(precise point positioning,PPP)动态解算,获得GNSS同震位移波形. 时间段选择为02:45:00—03:45:00(共18 000个历元). 由于本次地震为右旋走滑型地震[25],垂直方向波形较小,加之该方向精度较低,所以仅分析每个台站水平(E和N)方向的时间序列.
3. 震相识别结果与分析
3.1 CEEMD分解结果
为了验证本文方法在高频GNSS同震位移中P波初至拾取的可靠性,以p570台站E方向位移波形为例进行P波拾取,将TauP软件计算出地震波到达p570台站的理论到时作为可靠依据进行对比.
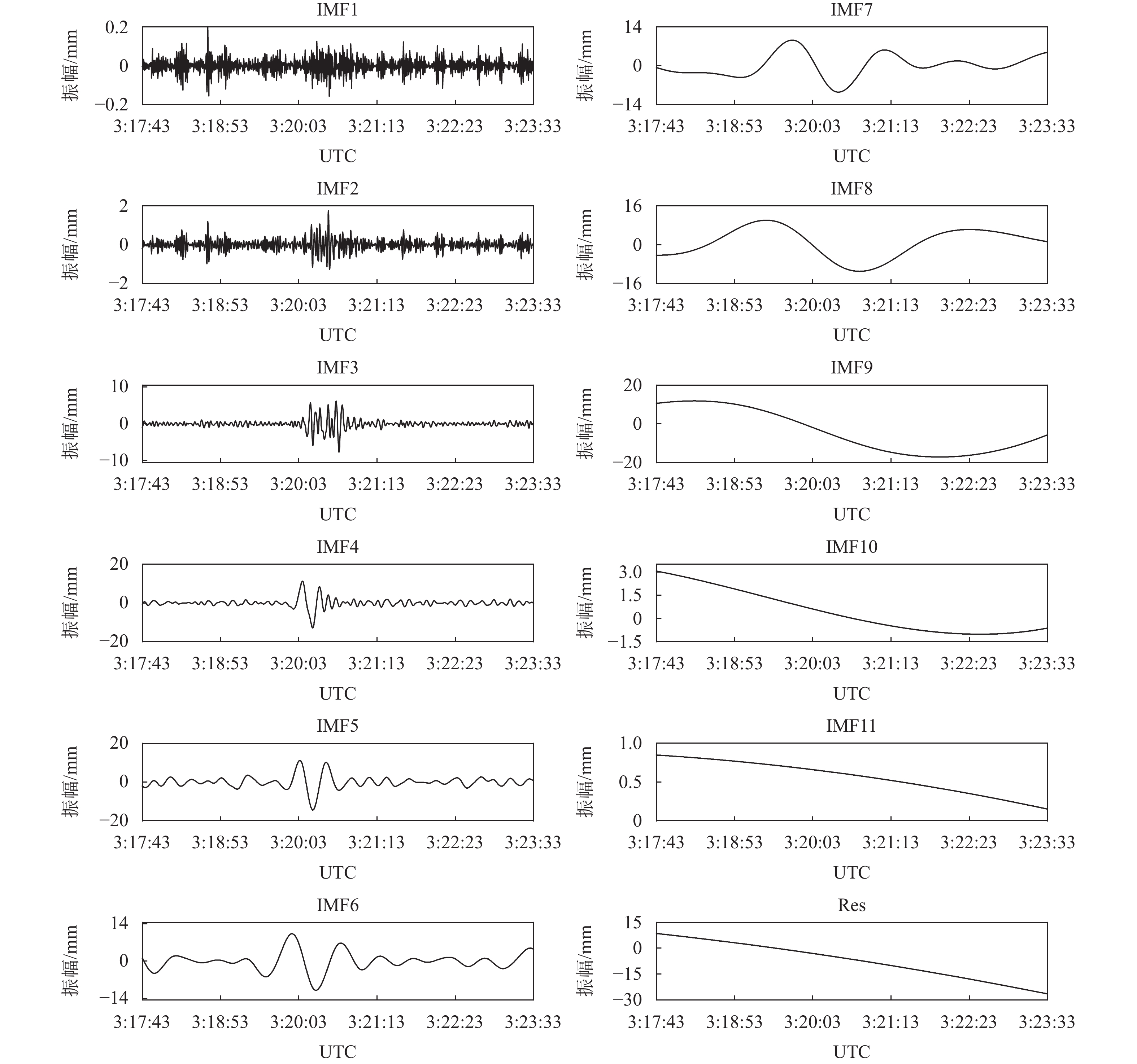
首先对位移波形进行小波降噪处理,经过多次尝试,参数选择为:db16小波基、软阈值去噪、2层分解,自适应阈值选择使用Stein的无偏风险估计原理确定. 图3给出的是p570台站E方向经小波降噪后的位移波形经CEEMD分解后得到的11个IMF分量和1个残余分量(Res). 从图3可以看出,IMF1~IMF3表现为相对高频分量,自IMF4开始高频震荡的分辨率逐渐降低,IMF5~IMF8表现出周期性变化,IMF9~IMF11为低频分量. 一般来说,IMF1分量主要包含高频白噪声,但经小波去噪后的该分量仍包含微弱的高频有效信息,所以在后续的分析中仍保留IMF1分量. 根据各IMF分量的MPE值,可将IMF1~IMF3分量视为高频分量,结果如表1所示.
表 1 p570台站E方向位移波形各IMF分量的MPE值模态分量 IMF1 IMF2 IMF3 IMF4 IMF5 IMF6 IMF7 IMF8 IMF9 IMF10 IMF11 MPE 0.829 9 0.772 8 0.758 8 0.513 8 0.329 2 0.229 0 0.164 1 0.130 3 0.109 5 0.114 4 0.108 4 3.2 高频GNSS同震波形P波初至拾取结果
TauP 软件是一款地震波走时计算器,可处理多种类型的速度模型,并能结合相位解析器计算几乎所有地震相位的走时[26]. 本文选择IASP 91速度模型计算P波理论到时[27],以此评定本文方法的拾取效果.
图4为对p570台站E方向原始位移波形的P波初至拾取过程. 根据Lee等[12]的描述,本文设置的IMER参数为:nt1取75个采样点,以包含所有的同震信号,nt2与nt3取700个采样点可有效的去除背景噪声的影响,移动平均滤波器的点数为10个采样点大小,阈值设置为1倍的IMER值的平均值. 根据图4(a)可看出,P波初至拾取到时与理论到时相差0.04 s,能够验证识别震相为P波. 图4(b)为重构波形的整体IMER值.
为进一步验证本文方法的拾取效果,将P波到时前后几秒的
$T_{(1,2)}^{{\text{MA}}}$ 、$T_{(1,3)}^{{\text{MA}}}$ 和IMER计算结果放大如图4(c)~(d)所示. 从图4(c)~(d)中可以看出,第一、三窗口计算的$T_{(1,3)}^{{\text{MA}}}$ 可减弱初至前的IMER值波动影响,有效减少了IMF1~IMF3分量中存在的高频噪声或复杂波动的影响,使高频GNSS拾取时刻与理论值更符合.图5 给出的是p570台站在E、N方向上高频GNSS同震位移及相应速度的P波初至拾取结果. 从波形上看,如图5(a)和图5(c)所示,原始速度波形无长周期趋势影响,但存在能量较大的高频噪声,掩盖了地震波振幅,而重构波形地震波振幅响应幅度明显增大. 从图5(b)和图5(d)可以看出,E和N方向原始位移波形捕捉到了地震波从震中向四周传播时产生的动态位移,但震前位移波形复杂,而重构波形消除了原始位移波形震前复杂波动的影响.
设置LTA/STA+ARAIC方法的短时窗宽取50个采样点,长时窗宽设置为短时窗宽的10倍,阈值设置为4,AR阶数为4,ARAIC前窗和后窗采样点数量分别为300和50. 对原始高频GNSS同震波形直接利用IMER和LTA/STA+ARAIC进行震相初至拾取,如图5(a)和图5(b)所示. 从两种方法的拾取结果上看,IMER方法在E、N原始速度和位移四种波形上的拾取结果与理论值差异的平均值和标准差分别为3.43 s和0.94 s,LTA/STA+ARAIC分别为4.34 s和2.13 s. 然而,对原始波形直接进行时域类震相识别时,IMER方法需要设置的阈值为 6 倍的IMER平均值,才能保证不会出现误拾取.
利用本文方法和C-LTA/STA+ARAIC对原始高频GNSS地震波形进行震相初至拾取,如图5(c)和图5(d)所示. 在E、N原始速度和位移四种波形上,本文方法的拾取结果与理论值差异的平均值和标准差分别为1.05 s和0.93 s,C-LTA/STA+ARAIC分别为2.27 s和1.21 s. 这表明本文方法优于C-LTA/STA+ARAIC,且对微弱信号的识别更有效,受噪声干扰的影响较小. 此外,与IMER与LTA/STA+ARAIC相比,本文方法和C-LTA/STA+ARAIC的拾取结果要优于前两者. 其原因是由于观测误差的存在以及台站方向的不同对地震波初至的敏感程度不同,可能会导致E、N方向的原始速度、位移波形地震响应表现存在较大差异,若直接利用时域类拾取方法难以适应所有波形,且阈值选取不合理时会产生错误拾取,而利用CEEMD分解尽可能地消除波形中的噪声,获得台站可靠的高频地震波,为震相初至的准确拾取提供有用的观测信息.
为了进一步验证本文方法在P波初至拾取的高效性,将14个台站在E、N方向的原始速度和位移波形分别记为TDCP_E、TDCP_N、PPP_E、PPP_N,利用本文方法、C-LTA/STA+ARAIC方法对四种波形进行初至拾取,结果如表2所示. 从表2可以看出,PPP_E拾取结果精度最高,PPP_N次之,这表明E方向比N方向PPP解算结果噪声更小;速度波形整体最差,原因可能是历元间载波相位差分解算时仅利用了GPS卫星,且未对接收机有关的误差进行有效改正,而PPP解算使用多系统、高精度轨道产品和钟差文件,得到的位移波形质量较高. 以理论P波到时为参考,通过分析四种波形拾取结果的均方根误差(root mean square error,RMSE)可以得出,本文方法拾取精度优于C-LTA/STA+ARAIC方法,这表明本文方法受噪声影响更小,能够适应大部分高频GNSS地震波形的拾取,P波初至拾取精度更高.
表 2 高频GNSS站点拾取到时及精度分析s 站点 Taup C-LTA/STA+ARAIC CEEMD-IMER P TDCP_E TDCP_N PPP_E PPP_N TDCP_E TDCP_N PPP_E PPP_N p594 4.28 6.4 6.8 4.4 4.4 5.0 1.6 4.2 2.6 cccc 4.31 6.2 3.2 7.6 7.8 5.8 2.2 4.0 3.6 p464 8.13 11.2 11.0 8.2 10.8 4.2 8.0 7.4 6.8 p593 9.65 16.0 14.0 8.6 12.4 15.0 14.2 10.6 12.0 p570 10.56 11.8 13.8 15.6 10.0 11.4 7.0 10.6 9.8 p569 11.18 17.2 17.6 12.2 12.0 17.2 16.6 12.0 12.0 p597 11.18 16.2 26.0 13.8 24.4 15.6 21.8 13.4 20.4 p592 11.18 16.8 17.2 11.0 17.8 16.4 14.6 11.2 16.0 p596 11.93 16.4 22.0 10.8 11.6 16.2 17.0 15.0 11.2 p568 13.95 12.4 22.8 14.0 15.6 18.2 22.6 14.8 15.6 p812 14.42 22.4 23.2 18.0 22.0 23.6 15.6 17.0 15.4 p591 14.42 27.6 23.6 17.2 22.4 20.2 23.0 17.2 22.0 p811 14.53 24.0 22.8 20.0 22.4 20.2 17.0 18.0 18.0 islk 14.76 16.8 23.6 15.8 19.2 14.6 18.2 15.6 14.2 RMSE 6.0 7.7 2.6 5.7 4.8 5.3 1.2 3.7 综上,本文方法的优势在于:1)经CEEMD分解后,可将初至拾取进行多尺度上的分析,探测出更微弱的同震信号,避免原始波形在初至前后能量差异较小时时域分析难以识别的问题;2)本文方法利用IMER方法中的三个检测窗口可较准确的拾取高频GNSS观测值中的微弱地震波,同时移动平均滤波器可以减弱复杂波动的影响.
4. 结束语
震相初至拾取是确定震中位置和建立地震目录所用的不同参数的关键. 然而,各种测量误差会导致原始短周期高频GNSS地震波形中存在复杂低频波动和高频噪声. 对此,本文提出了联合CEEMD和IMER的高频GNSS同震位移P波震相识别方法,以提高高频GNSS同震波形P波初至的拾取精度.
利用该方法对美国加利福尼亚州Ridgecrest地区震时台站的高频GNSS同震记录的速度波形和位移波形进行P波震相的自动拾取. 结果表明,相较于IMER、LTA/STA+ARAIC方法,本文方法可显著减小高频GNSS噪声以及非线性变化的影响. 与C-LTA/STA+ARAIC方法相比,本文方法P波初至拾取的精度更高,对微弱信号的识别更有效,受噪声干扰的影响较小. 因此,本文方法可有效克服高频GNSS同震位移存在的低信噪比、非平稳性等缺陷,有效提高P波初至拾取的自适应性,提升拾取结果的精度,降低错误拾取的概率,可为地震预警、震后灾害快速评估提供支持和依据.
-
表 1 p570台站E方向位移波形各IMF分量的MPE值
模态分量 IMF1 IMF2 IMF3 IMF4 IMF5 IMF6 IMF7 IMF8 IMF9 IMF10 IMF11 MPE 0.829 9 0.772 8 0.758 8 0.513 8 0.329 2 0.229 0 0.164 1 0.130 3 0.109 5 0.114 4 0.108 4 表 2 高频GNSS站点拾取到时及精度分析
s 站点 Taup C-LTA/STA+ARAIC CEEMD-IMER P TDCP_E TDCP_N PPP_E PPP_N TDCP_E TDCP_N PPP_E PPP_N p594 4.28 6.4 6.8 4.4 4.4 5.0 1.6 4.2 2.6 cccc 4.31 6.2 3.2 7.6 7.8 5.8 2.2 4.0 3.6 p464 8.13 11.2 11.0 8.2 10.8 4.2 8.0 7.4 6.8 p593 9.65 16.0 14.0 8.6 12.4 15.0 14.2 10.6 12.0 p570 10.56 11.8 13.8 15.6 10.0 11.4 7.0 10.6 9.8 p569 11.18 17.2 17.6 12.2 12.0 17.2 16.6 12.0 12.0 p597 11.18 16.2 26.0 13.8 24.4 15.6 21.8 13.4 20.4 p592 11.18 16.8 17.2 11.0 17.8 16.4 14.6 11.2 16.0 p596 11.93 16.4 22.0 10.8 11.6 16.2 17.0 15.0 11.2 p568 13.95 12.4 22.8 14.0 15.6 18.2 22.6 14.8 15.6 p812 14.42 22.4 23.2 18.0 22.0 23.6 15.6 17.0 15.4 p591 14.42 27.6 23.6 17.2 22.4 20.2 23.0 17.2 22.0 p811 14.53 24.0 22.8 20.0 22.4 20.2 17.0 18.0 18.0 islk 14.76 16.8 23.6 15.8 19.2 14.6 18.2 15.6 14.2 RMSE 6.0 7.7 2.6 5.7 4.8 5.3 1.2 3.7 -
[1] 张小红, 郭斐, 郭博峰, 等. 利用高频GPS进行地表同震位移监测及震相识别[J]. 地球物理学报, 2012, 55(6): 1912-1918. DOI: 10.6038/j.issn.0001-5733.2012.06.012 [2] 王杰民, 殷海涛. 基于S变换的高频全球导航卫星系统同震数据的震相识别研究[J]. 地震学报, 2018, 40(6): 753-759. DOI: 10.11939/jass.20180029 [3] 张环宇, 林吉航, 陈庭. 利用高频GPS数据反演地震要素[J]. 全球定位系统, 2020, 45(6): 37-45. [4] SHA'AMERI A Z, ARIS W A W, SADIAH S, et al. Reliability of seismic signal analysis for earthquake epicenter location estimation using 1 Hz GPS kinematic solution[J]. Measurement, 2021(182): 109669. DOI: 10.1016/j.measurement.2021.109669
[5] 李康, 蒋光伟, 高春伟, 等. 基于GNSS的青海玛多M7.4级地震的地表形变分析[J]. 全球定位系统, 2022, 47(2): 66-72. DOI: 10.12265/j.gnss.2021081803 [6] 张文浩, 尹玲, 胡文博. 基于多台站高频GPS的地震预警优化算法研究[J]. 全球定位系统, 2022, 47(3): 56-64. DOI: 10.12265/j.gnss.2021120205 [7] 王旭科, 陈良周, 姚伟. 基于GNSS的2023年8月德州平原县5.5级地震异常环境响应分析[J]. 全球定位系统, 2024, 49(2): 76-81. DOI: 10.12265/j.gnss.2023219 [8] SAAD O M, INOUE K, SHALABY A, et al. Automatic arrival time detection for earthquakes based on stacked denoising autoencoder[J]. IEEE geoscience and remote sensing letters, 2018, 15(11): 1687-1691. DOI: 10.1109/LGRS.2018.2861218
[9] WANG Z J, ZHAO B M. Applicability of accurate ground motion estimation using initial P wave for earthquake early warning[J]. Frontiers in earth science, 2021(9): 718216. DOI: 10.3389/feart.2021.718216
[10] STEVENSON P R. Microearthquakes at flathead lake, montana: a study using automatic earthquake processing[J]. Bulletin of the seismological society of america, 1976, 66(1): 61-80. DOI: 10.1785/BSSA0660010061
[11] SLEEMAN R, VAN E T. Robust automatic P-phase picking: an on-line implementation in the analysis of broadband seismogram recordings[J]. Physics of the earth and planetary interiors, 1999, 113(1-4): 265-275. DOI: 10.1016/S0031-9201(99)00007-2
[12] LEE M H, BYUN J, KIM D W, et al. Improved modified energy ratio method using a multi-window approach for accurate arrival picking[J]. Journal of applied geophysics, 2017(139): 117-130. DOI: 10.1016/j.jappgeo.2017.02.019
[13] KUDŁACIK I, KAPŁON J, KAZMIERSKI K, et al. First feasibility demonstration of GNSS-seismology for anthropogenic earthquakes detection[J]. Scientific reports, 2023, 13(1): 20905. DOI: 10.1038/s41598-023-47964-2
[14] 李艳艳, 殷海涛, 韩林桥. 利用MSMPCA去噪的CEEMD方法监测高频GNSS同震形变[J]. 武汉大学学报(信息科学版), 2022, 47(3): 352-360. [15] LI X, SHANG X, MORALES-ESTEBAN A, et al. Identifying P phase arrival of weak events: the akaike information criterion picking application based on the empirical mode decomposition[J]. Computers & geosciences, 2017(100): 57-66. DOI: 10.1016/j.cageo.2016.12.005
[16] YEH J-R, SHIEH J-S, HUANG N E. Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method[J]. Advances in adaptive data analysis, 2010, 2(2): 135-156. DOI: 10.1142/S1793536910000422
[17] 高清文, 赵国忱. CEEMD与GRNN神经网络电离层TEC预报模型[J]. 全球定位系统, 2021, 46(4): 76-84. DOI: 10.12265/j.gnss.2020091401 [18] 姚依欣, 王勇, 詹金刚, 等. 利用平滑先验信息方法分离高频GPS数据静态永久变形与地震波[J]. 测绘学报, 2018, 47(4): 490-497. DOI: 10.11947/j.AGCS.2018.20160648 [19] 马晓燕, 王文波. 联合同步挤压小波变换和多尺度排列熵的局部放电类型识别[J]. 计算机测量与控制, 2020, 28(2): 131-135. [20] 李志才, 陈智, 武军郦, 等. 基于高频GNSS观测的甘肃积石山6.2级地震同震形变[J/OL].(2024-01-15). 武汉大学学报(信息科学版), 2025: 1-13. https://link.cnki.net/doi/10.13203/j.whugis20240004 [21] 张炎亮, 李营. 基于多尺度排列熵和IWOA-SVM的滚动轴承故障诊断[J]. 电子测量技术, 2023, 46(19): 29-34. [22] 郑近德, 程军圣, 杨宇. 改进的EEMD算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21-26,46. DOI: 10.3969/j.issn.1000-3835.2013.21.004 [23] CROWELL B W. Near-field strong ground motions from GPS‐derived velocities for 2020 intermountain western united states earthquakes[J]. Seismological research letters, 2021, 92(2A): 840-848. DOI: 10.1785/0220200325
[24] GENG J H, YANG S F, GUO J. Assessing IGS GPS/Galileo/BDS-2/BDS-3 phase bias products with PRIDE PPP-AR[J]. Satellite navigation, 2021, 2(1): 1-15. DOI: 10.1186/s43020-021-00049-9
[25] 马振宁, 钱荣毅, CATCHINGS R, 等. 美国南加州Ridgecrest M_W6.4-M_W7.1地震地表破裂几何学及运动学特征[J]. 地球物理学报, 2021, 64(4): 1206-1214. DOI: 10.6038/cjg2021O0061 [26] CROTWELL H P, OWENS T J, RITSEMA J. The TauP toolkit: flexible seismic travel-time and ray-path utilities[J]. Seismological research letters, 1999, 70(2): 154-160. DOI: 10.1785/gssrl.70.2.154
[27] MATTIOLI G S, PHILLIPS D A, HODGKINSON K M, et al. The GAGE data and field response to the 2019 Ridgecrest earthquake sequence[J]. Seismological research letters, 2020, 91(4): 2075-2086. DOI: 10.1785/0220190283



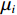

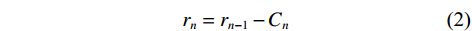
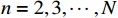

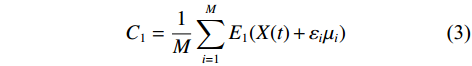

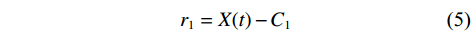
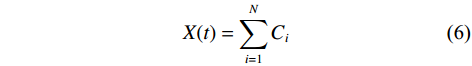
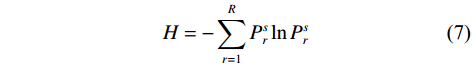
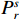

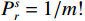
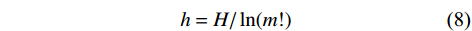


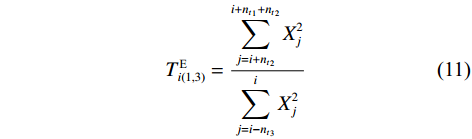
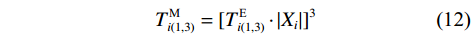
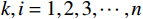
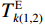
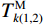
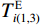
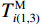
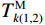
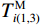

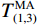
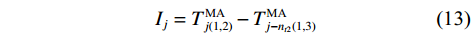

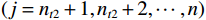
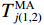
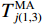
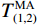


 下载:
下载: