Path planning of intelligent aircraft based on linear matrix inequality
-
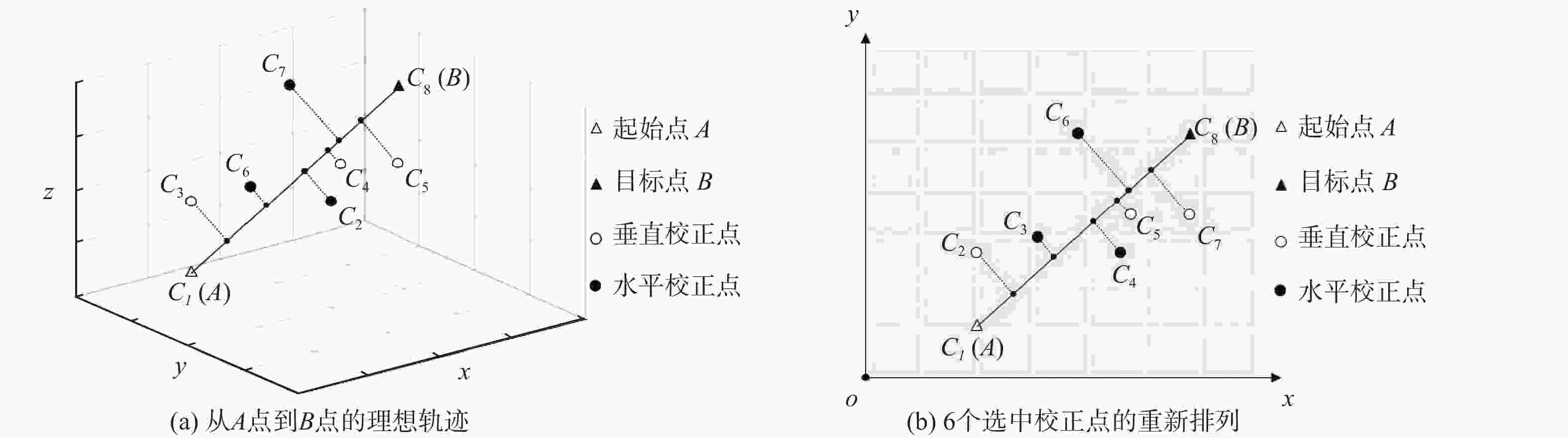
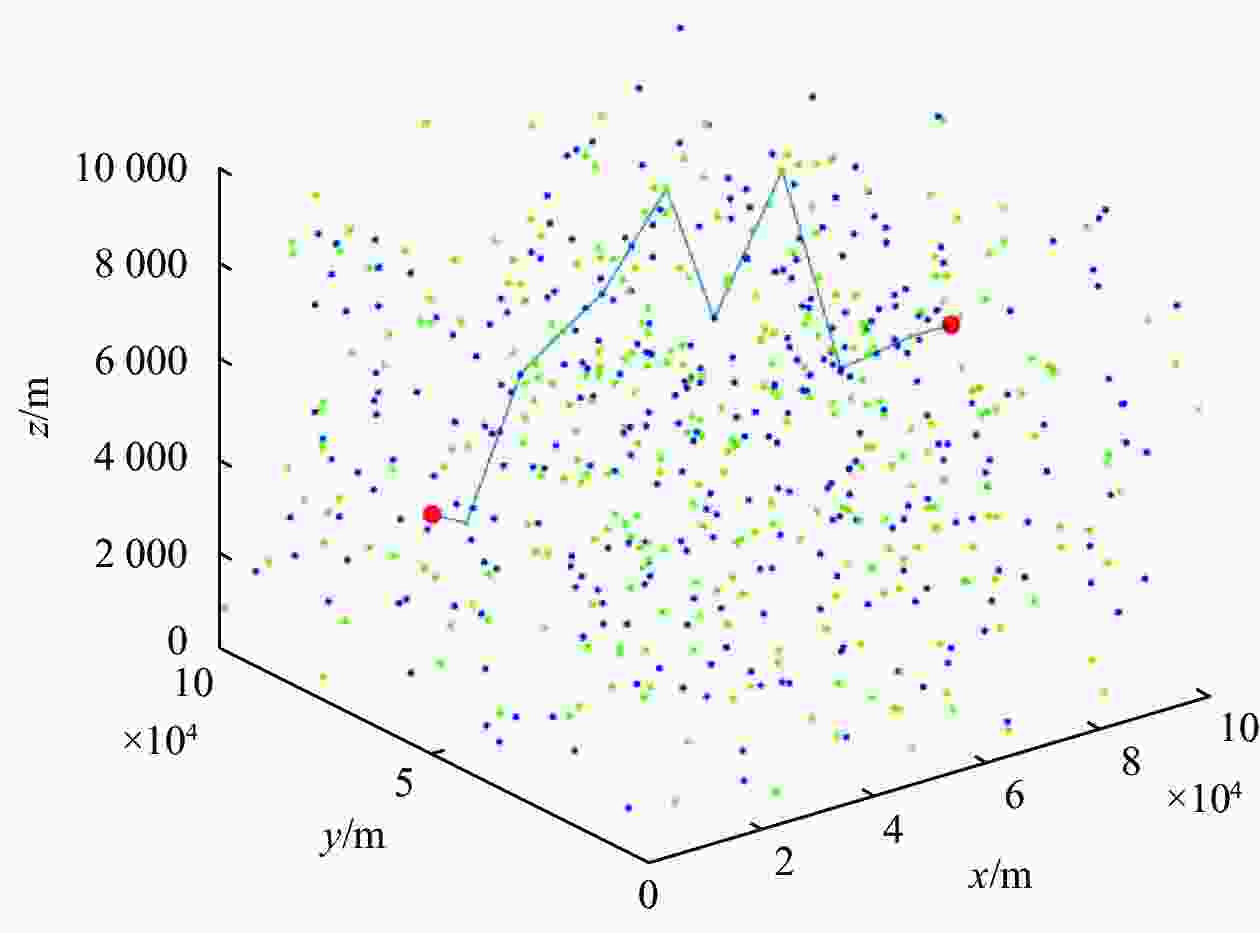
摘要: 智能飞行器在军用和民用领域发挥着越来越重要的作用. 在飞行过程中经常会出现累积的定位误差并且飞行到达应用场景时有定位精度要求,故需要对飞行轨迹进行适当的位置校正. 为此,提出了一种在复杂条件下的智能飞行器航迹规划方法,利用基于线性矩阵不等式(LMI)的优化方法实现最少校正次数和最短飞行距离的双重目标. 根据可用校正点数量以及它们对飞行器位置的不同影响,首先生成一个0~1三角变量矩阵来表示从点A开始的飞行航迹,以面向目标的方式不重复的遍历一系列校正点,并最终到达目标点;然后对航迹相关矩阵的变量项施加强制性的约束条件,将所有的约束作为一个整体转换和施加到之前定义的变量矩阵中,最后利用基于LMI的优化方法实现双重优化. 通过仿真结果验证了所提出的航迹规划方法在计算资源和优化结果方面比线性规划等其他优化方法更优越.
-
关键词:
- 线性矩阵不等式(LMI) /
- 航迹规划 /
- 水平校正 /
- 垂直校正 /
- 校正点
Abstract: Intelligent aircraft plays an increasingly important role in a variety of applications. The aircraft's position accuracy while arriving at the application scenery is required. And it necessitates the flight's trajectory planning with appropriate position corrections due to the accumulated position errors that usually occur during the flight. To this end, this paper proposes a trajectory planning method for an intelligent aircraft working in some complex conditions, where an linear matrix inequality (LMI)-based optimizing method is utilized to achieve the dual goal of minimum correction times and minimum travel length. According to the number of available correction points and their different influences on the aircraft position, a triangular variable matrix with 0-1 entries is first designed to represent a flight trajectory that starts from point A, traverses a series of correction points in a target-oriented manner without any repetition, and ultimately arrives at the target point. After that, several other compulsory constranits are imposed on the trajectory-related matrix's variable entries, all of these constranits are later transformed and imposed on the previously defined variable matrix as a whole. The LMI-based optimizing method is performed to achieve the dual goal. Simulational results validate the proposed trajectory planning method and demonstrate its remarkable performance in the sense of less computing resources and optimization results, compared with many other optimization methods such as linear pro-gramming. -
表 1 常用符号含义
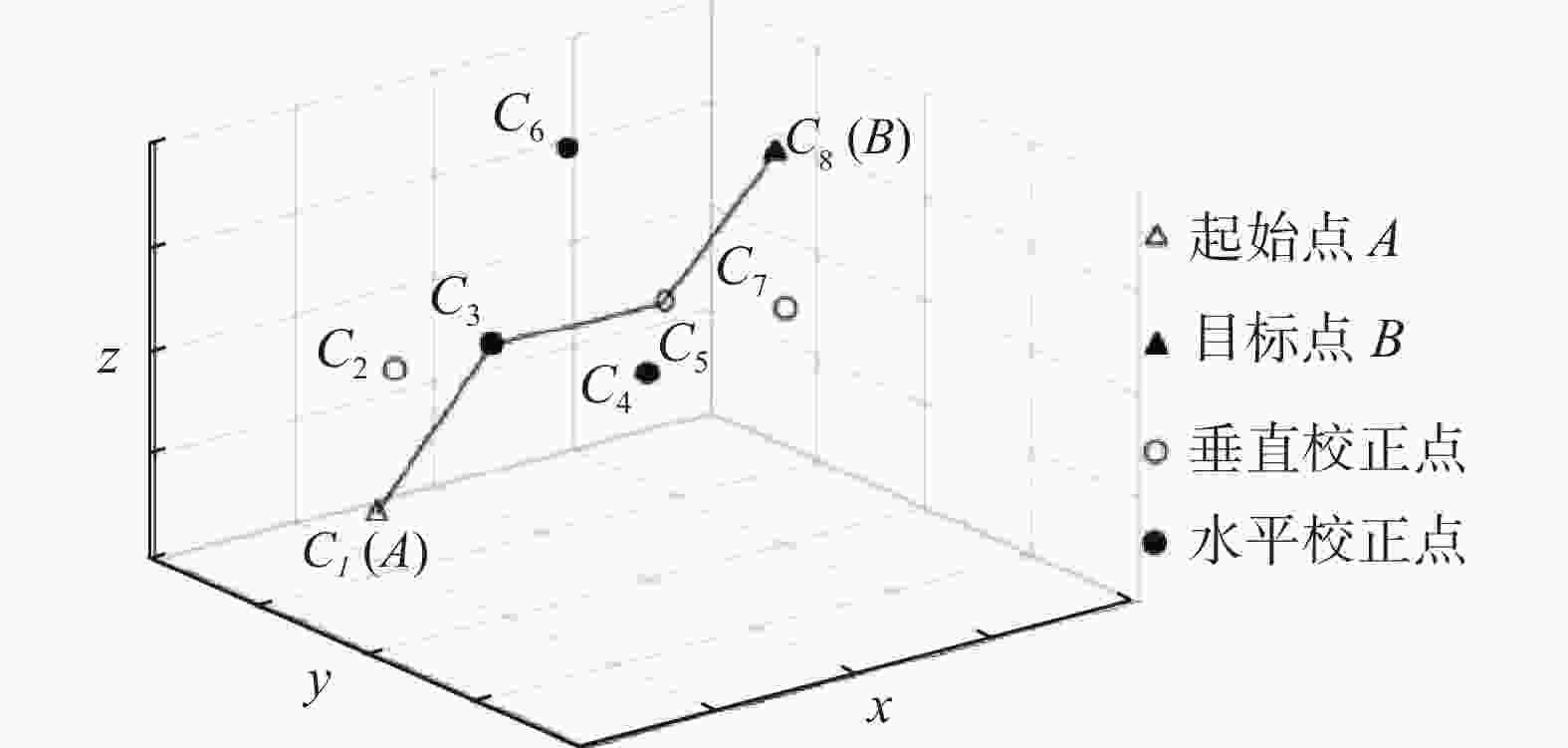
符号 符号含义 A 出发点A B 目标点B $ {x}_{ij} $ 0~1变量 $ {\alpha }_{1} $ 垂直校正点的垂直误差上界 $ {\alpha }_{2} $ 垂直校正点的水平误差上界 ${\;\beta }_{1}$ 水平校正点的垂直误差上界 ${\;\beta }_{2}$ 水平校正点的水平误差上界 $ \theta $ 终点的垂直与水平误差上界 $ \delta $ 飞行器飞行1 m产生的误差 $ {d}_{ij} $ 校正点$ i $与校正点$ j $之间的欧式距离 表 2 图3所示规划后轨迹的变量矩阵
变量
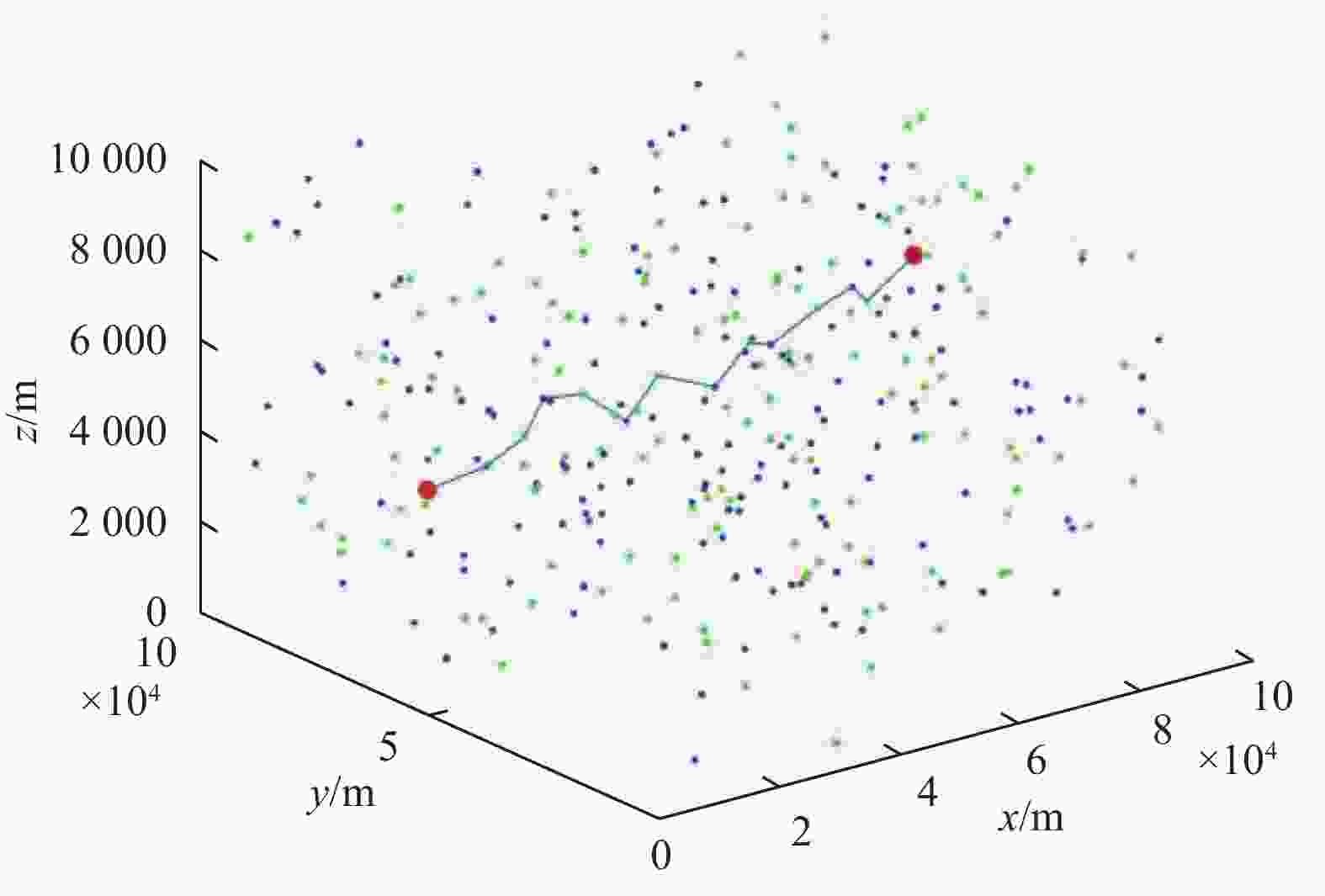
矩阵C1(A) C2 C3 C4 C5 C6 C7 C8(B) C1(A) 0 0 1 0 0 0 0 0 C2 0 0 0 0 0 0 0 0 C3 0 0 0 0 1 0 0 0 C4 0 0 0 0 0 0 0 0 C5 0 0 0 0 0 0 0 1 C6 0 0 0 0 0 0 0 0 C7 0 0 0 0 0 0 0 0 C8(B) 0 0 0 0 0 0 0 0 表 3 航迹规划结果
m 校正点
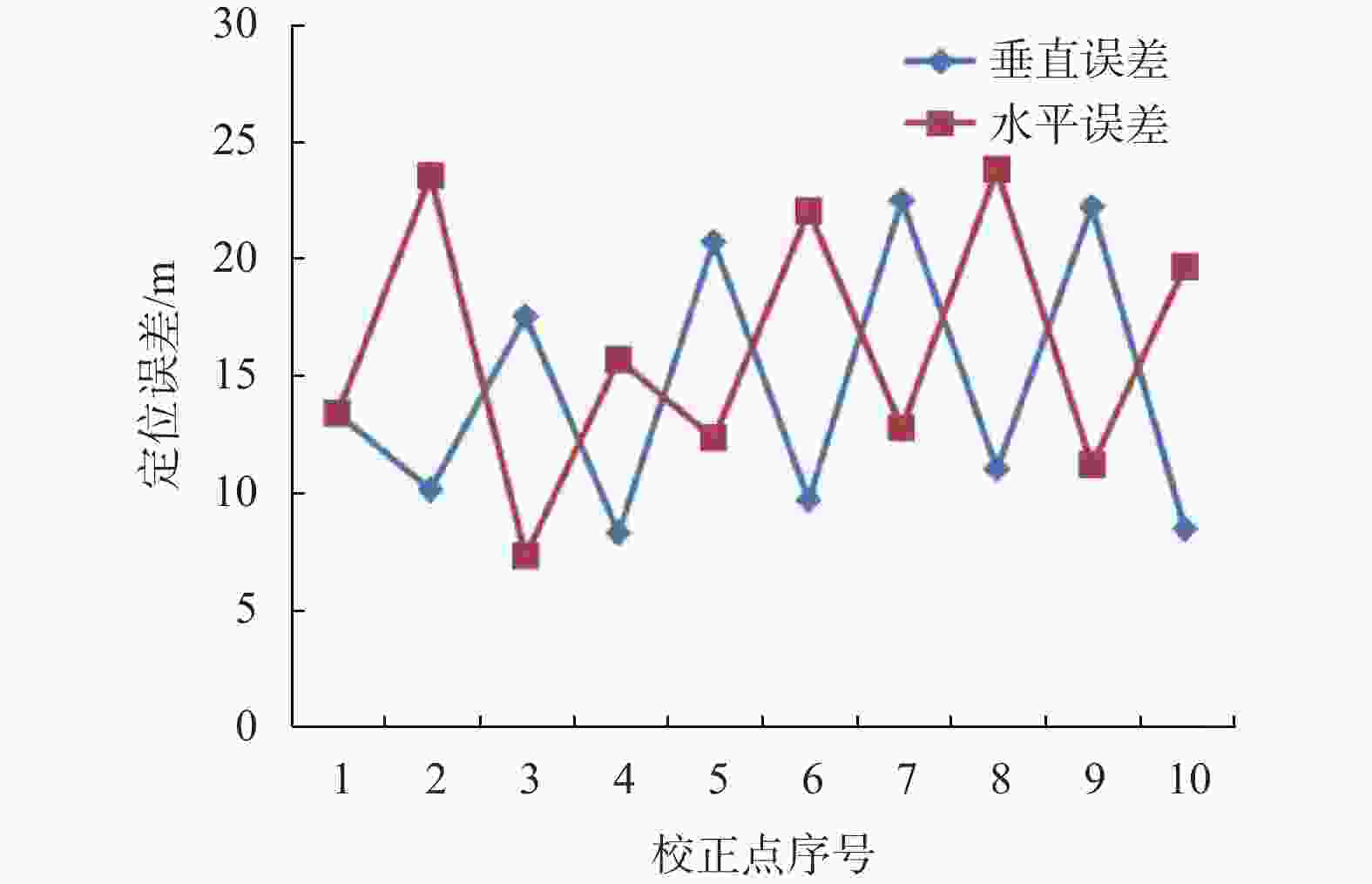
编号校正前的
垂直误差校正前的
水平误差校正点
类型A 0 0 A 504 13.39 13.39 1 295 10.18 23.57 0 92 17.53 7.35 1 608 8.35 15.70 0 90 20.72 12.37 1 12 9.69 22.06 0 404 22.53 12.84 1 595 11.03 23.87 0 502 22.23 11.20 1 B 8.49 19.69 B 表 4 算法性能指标
算法名称 校正点数量 航迹长度/m 误差是否满足要求 LMI 9 104890.550 是 Dijkstra算法 10 104562.940 是 GA 9 106837.970 是 目标导引法 9 111286.498 是 表 5 航迹规划结果
m 校正点
编号校正前的
垂直误差校正前的
水平误差校正点
类型A 0 0 A 163 13.29 13.29 0 114 18.62 5.33 1 8 13.92 19.26 0 309 19.45 5.52 1 305 5.97 11.49 0 123 15.17 9.20 1 45 10.01 19.21 0 160 17.49 7.49 1 92 5.78 13.26 0 93 15.26 9.48 1 61 9.83 19.32 0 292 16.39 6.55 1 B 6.96 13.51 B -
[1] ZHANG C, ZHEN Z Y, WANG D B, et al. UAV path planning method based on ant colony optimization[C]//Chinese Control and Decision Conference, 2010. DOI: 10.1109/CCDC.2010.5498477 [2] YANG Q, YOO S J. Optimal UAV path planning: sensing data acquisition over IoT sensor networks using multi-objective bio-inspired algorithms[J]. IEEE access, 2018(99): 1. DOI: 10.1109/ACCESS.2018.2812896 [3] ASADI S, AZIMIRAD V, ESLAMI A, et al. A novel global optimal path planning and trajectory method based on adaptive Dijkstra-immune approach for mobile robot[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 2011. DOI: 10.1109/AIM.2011.6027073 [4] 李昱奇, 刘志乾, 程凝怡, 等. 多约束条件下无人机航迹规划[J]. 计算机工程与应用, 2020, 57(4): 225-230. DOI: 10.3778/j.issn.1002-8331.1810-0410 [5] KALA R, SHUKLA A, TIWARI R. Fusion of probabilistic A* algorithm and fuzzy inference system for robotic path planning[J]. Artificial intelligence review, 2010, 33(4): 307-327. DOI: 10.1007/s10462-010-9157-y [6] WANG Y, CAI F, WANG Y. Dynamic path planning for mobile robot based on particle swarm optimization[J]. AIP conference proceedings, 2017, 1864(1): 20024. DOI: 10.1063/1.4992841 [7] CHENG Z, WANG E G, TANG Y X, et al. Real-time path planning strategy for UAV based on improved particle swarm optimization[J]. Journal of computers, 2014, 9(1): 209-214. DOI: 10.4304/jcp.9.1.209-214 [8] CHEN Y B, LUO G C, MEI Y S, et al. UAV path planning using artificial potential field method updated by optimal control theory[J]. International journal of systems science, 2016, 47(6): 1407-1420. DOI: 10.1080/00207721.2014.929191 [9] SEO W J, OK S H, AHN J H, et al. An efficient hardware architecture of the A-star algorithm for the shortest path search engine[C]// The 5th International Joint Conference on INC, IMS and IDC, 2009. DOI: 10.1109/NCM.2009.371 [10] CARSTEN J, FERGUSON D, STENTZ A. 3D field D: improved path planning and replanning in three dimensions[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, 2006: 3381-3386. DOI: 10.1109/IROS.2006.282516 [11] CULLIGAN K, VALENTI M, KUWATA Y, et al. Three-dimensional flight experiments using on-line mixed-integer linear programming trajectory optimization[C]//American Control Conference, 2007. DOI: 10.1109/ACC.2007.4283101 [12] KOU X L, LIU S Y, ZHANG J K, et al. Co-evolutionary particle swarm optimization to solve constrained optimization problems[J]. Computers and mathematics with applications, 2009, 57(11-12): 1776-1784. DOI: 10.1016/j.camwa.2008.10.013 [13] 方群, 徐青. 基于改进粒子群算法的无人机三维航迹规划[J]. 西北工业大学学报, 2017, 35(1): 66-73. DOI: 10.3969/j.issn.1000-2758.2017.01.011 [14] HAO Z, XIONG H L, LIU Y, et al. Trajectory planning algorithm of UAV based on system positioning accuracy constraints[J]. Electronics, 2020, 9(2): 250. DOI: 10.3390/electronics9020250 -



 下载:
下载: